练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    等腰三角形中，一个角为50°，则这个等腰三角形的顶角的度数为（　　）

    A. 150° B. 80° C. 50°或80° D. 70°

    C 【解析】若50°是底角，则顶角为：180°?50°×2=80°； 若50°为顶角，所以顶角的度数为50°或80°. 故选：C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（C卷） 题型：解答题

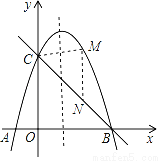
    如图，抛物线y=﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，已知A（﹣1，0），C（0，3）

    （1）求该抛物线的表达式；

    （2）求BC的解析式；

    （3）点M是对称轴右侧点B左侧的抛物线上一个动点，当点M运动到什么位置时，△BCM的面积最大？求△BCM面积的最大值及此时点M的坐标．

    （1）抛物线的解析式y=-x2+2x+3；（2）BC的解析式为y=-x+3；（3）△BCM面积的最大值为，此时点M的坐标（， ）． 【解析】试题分析： （1）将A、C坐标代入y=﹣x2+bx+c列方程组求得b、c的值即可求得解析式； （2）由（1）中所求解析式可求得B的坐标，结合点C的坐标，用待定系数法可求得直线BC的解析式； （3）过点M作MN∥y轴，交BC于点N，设点M...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷（A卷） 题型：填空题

    试写出一个含有未知数x的一元二次方程________．

    -2x+1=0 【解析】据一元二次方程的定义，只含有一个未知数，且最高次为2次的整式方程.答案不唯一.

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级（上）第一次月考数学试卷 题型：解答题

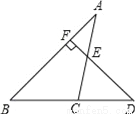
    如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，∠A=35°，∠D=42°，求∠ACD的度数．

    ∠ACD的度数为83°． 【解析】试题分析：根据三角形外角与内角的关系及三角形内角和定理解答． 试题解析：因为∠AFE=90°,所以∠AEF=90°-∠A=90°-35°=55°. 所以∠CED=∠AEF=55°, 所以∠ACD=180°-∠CED-∠D=180°-55°-42=83°

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年八年级（上）第一次月考数学试卷 题型：填空题

    一个等腰三角形有两边分别为5cm和8cm，则周长是 厘米.

    18或21 【解析】本题考查了等腰三角形的性质和三角形的三边关系 题目给出等腰三角形有两条边长为5cm和8cm，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形． ∵等腰三角形两边为5和8厘米 ∴等腰三角形三边可能为5，5，8或5，8，8 ∴周长可能为18或21厘米．

    查看答案和解析>>

    科目：初中数学 来源：广西南宁市2017年中考数学一模试卷 题型：解答题

    如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C．

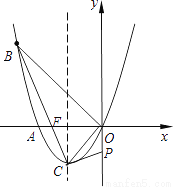
    （1）求抛物线的函数解析式．

    （2）设点D在抛物线上，点E在抛物线的对称轴上，若四边形AODE是平行四边形，求点D的坐标．

    （3）联接BC交x轴于点F．y轴上是否存在点P，使得△POC与△BOF相似？若存在，求出点P的坐标；若不存在，请说明理由．

    (1) y=x2+2x;(2) （1，3）;(3) （0，﹣ ）或（0，﹣4）． 【解析】试题分析：（1）将点A、点B和原点代入解析式进行求解；（2）根据平行四边形的性质得出点D的坐标；（3）首先求出OB、OF、OC的长度，然后根据三角形相似的条件求出点P的坐标，分两种情况进行讨论. 试题解析：（1）设抛物线的解析式为y=ax2+bx+c（a≠0）， 将点A（﹣2，0），B（﹣3...

    查看答案和解析>>

    科目：初中数学 来源：广西南宁市2017年中考数学一模试卷 题型：解答题

    计算：﹣12+6sin60°﹣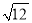+20170 ．

    【解析】试题分析：原式利用乘方的意义，特殊角的三角函数值，二次根式性质，以及零指数幂法则计算即可得到结果． 试题解析：原式=﹣1+3﹣2+1=.

    查看答案和解析>>

    科目：初中数学 来源：广西南宁市2017年中考数学一模试卷 题型：单选题

    ﹣2的相反数是（   ）

    A. 2 B. ﹣2   C. 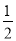  D. ﹣

    A 【解析】试题解析：根据相反数的定义，-2的相反数是2． 故选A．

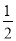
    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市江夏区2017-2018学年八年级（上）期中数学试卷 题型：单选题

    在△ABC中，AC=BC，∠ACB=90°，CE是过C点的一条直线，AD⊥CE于D，BE⊥CE于E，DE=4cm，AD=2cm，则BE=（　　）

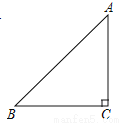
    A. 2cm B. 4cm C. 6cm或2cm D. 6cm

    C 【解析】试题解析：分为两种情况： ①如图1，当CE在△ABC内． ∵AD⊥CE，∠BCA=90°， ∴∠ADC=∠BCA=90°， ∴∠DCA+∠BCE=90°，∠DCA+∠DAC=90°， ∴∠DAC=∠BCE， ∵AD⊥CE，BE⊥CE， ∴∠ADC=∠BEC=90°， 在△ACD和△CBE中， ， ∴△ACD≌△CBE（A...

    查看答案和解析>>

    同步练习册答案