
��һ������У��У��Ȱ���31��ȥ�βݣ�18��ȥֲ������������20��ȥ֧Ԯ���ǣ�����βݵ�������ֲ����������2������֧Ԯ�βݺ�ֲ���ķֱ��ж����ˣ���ֻ�г����̼��ɣ�
31��x��2[18����20��x��]�� �������������������֧Ԯ�βݵ���x�ˣ���֧Ԯֲ�����У�20-x���ˣ����ݵ�����ϵ��ԭ���β�����+֧Ԯ�βݵ�����=2����ԭ��ֲ��������+֧Ԯֲ�������������з��̼��ɣ� �����������֧Ԯ�βݵ���x�ˣ�������ã�31+x=2[18+��20-x��]��
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�������������ѧ�Ծ����꼶��11.3 ����μ����ڽǺ͡�ͬ������ ���ͣ������
���һ������γ���һ���ڽ����⣬�����ڽǵĺ�Ϊ2570�㣬�����û�м������ڵ��ڽǵĶ�����
130�� �����������������������ڽ�Ϊx�����ݶ���ε��ڽǺ�ʽ��n��2��•180���֪������ε��ڽǶ�����180��ı�����Ȼ���������������Խ�����⣮ ����������������� ���������εı�����n��û�м������ڵ��ڽǵĶ�����x����n��2��•180��=2570��+x��n=16��50�㣬180�㩁50��=130�㣬������������17���Σ�û�м������ڵ��ڽǵĶ���Ϊ130�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ� 22.3 ���κ�����Ӧ�� ͬ������ ���ͣ���ѡ��
��������Ա��ſ���ȥ����ĸ߶���ʱ��ı仯���仯����һ���̿ɽ��Ƶ��������ķ�ͼ�̻���������
A. 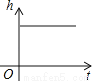 B.
B. 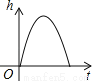 C.
C. 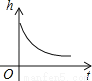 D.
D. 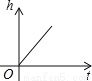
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�ij���2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ��һ��DZͧ�ں�����500��A����ø���Ϊ30��ĺ���C����һ��ϻ�ӷ����źţ�������ͬһ���ֱ�ߺ���4000����B����ø���Ϊ60��ĺ���Ҳ�иú�ϻ�ӷ������źţ����ϻ������λ�õ�C�ں����µ����Ϊ�� ��
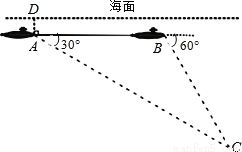
A. 2000�� B. 4000�� C. 2000�� D. ��2000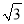 +500����
+500����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�ij���2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
���з����У���һԪ���η��̵��ǣ�������
A. 2x-y=3 B. x2+ =2 C. x2+1=x2-1 D. x��x-1��=0
=2 C. x2+1=x2-1 D. x��x-1��=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ�5.3Ӧ��һԪһ�η���--ˮ�����˿�ʱ��ϰ���������� ���ͣ������
ij��������һ��������ƻ���20������ɣ���ÿ�������4������15������һ�������10������ԭ�ƻ�ÿ������x��������������з���Ϊ______��
20x��15��x��4����10�� �����������ݵ�����ϵ:ʵ��15����ɵ������ȼƻ�20����ɵ�������10��,��ԭ�ƻ�ÿ������x��,ԭ�ƻ�20����������Ϊ:20x,ʵ��15������������Ϊ:15(x+4),����������г�����Ϊ: 20x��15��x��4����10,�ʴ�Ϊ: 20x��15��x��4����10.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ�5.3Ӧ��һԪһ�η���--ˮ�����˿�ʱ��ϰ���������� ���ͣ���ѡ��
Ϊ�����ֳ��У��γ��н��Գ������ɵ������̻����ƻ���ijһ�ι�·��һ��ȫ�����Ϲ�����Ҫ��·�����˸���һ�ã�����ÿ�������ļ����ȣ����ÿ��6����1�ã�������ȱ22�ã����ÿ��7����1�ã��������������꣮��ԭ������x�ã�����������г�������ȷ���ǣ� ��
A. 6��x��22����7��x��1�� B. 6��x��22��1����7��x��1��
C. 6��x��22��1����7x D. 6��x��22����7x
B �������������������ԭ������x�ã������ס�β���˾���������ÿ���6����һ�ã���ȱ��22�ã���֪��һ�ι�·��Ϊ6��x+22��1������ÿ��7����1�ã��������������꣬��֪��һ�ι�·���ֿ��Ա�ʾΪ7��x��1�������ݹ�·�ij��Ȳ����г����̼��ɣ� �������� ��ԭ������x�ã�������� 6��x+22��1��=7��x��1���� ��ѡ��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶��ѧ�ϲ� ��23�� ��ת ͬ����Ԫ����Ծ���Word�渽�𰸣� ���ͣ������
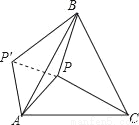
��ͼ��P����������ABC�ڵ�һ�㣬��PA=6��PB=8��PC=10��������PAC�Ƶ�A��ʱ����ת��õ���P��AB��
��1�����P���P��֮��ľ��룻
��2�����APB�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���˽̰��꼶��ѧ�ϲ� ��14�� ��ĩ�ۺϼ�� ���ͣ������
���㣺��1��992-102��98;
��2����x��x2y2-xy��-y��x2-x3y���ݡ�x2y.
���𰸡���1��-195��2��2xy-2
�������������������1������ƽ���ʽ����ȫƽ����ʽ������.
(2)��ȡ����ʽ������.
���������
��1��ԭʽ=��100-1��2-��100+2������100-2��
=��1002-200+1��-��1002-4��=-200+5=-195.
��2��ԭʽ=��x2y��xy-1��-x2y��1-xy���ݡ�x2y
=2x2y��xy-1����x2y=2��xy-1��=2xy-2.
�����͡������
��������
21
��1���Ȼ�������ֵ��a��a-2b��+��a+b��2������a=-1��b=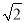 ;
;
��2����x2-5x=3����x-1����2x-1��-��x+1��2+1��ֵ.
��1��ԭʽ= 2a2+b2=2+2=4����2��ԭʽ=4. �����������������(1)������ȫƽ����ʽչ������������ֵ. (2) ������ȫƽ����ʽչ�����������������ֵ. �⣺��1��ԭʽ=a2-2ab+a2+2ab+b2=2a2+b2. ��a=-1��b=ʱ��ԭʽ=2+2=4. ��2��ԭʽ=2x2-3x+1-��x2+2x+1��+1=x2-5x+1=3+1=4.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com