练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

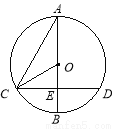
    如图，⊙O的直径AB与弦CD（不是直径）交于点E，且CE=DE，∠A=30°，OC = 4，那么CD的长为

    A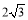． B．4 C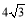． D．8

    C 【解析】 试题分析：因为CE=DE，AB是⊙O的直径，所以CD AB, 又∠A=30°，OA=OC=4,所以∠COE=60°，所以在Rt△COE中，CE=OCsin60°=4×=2，所以CD=2CE=,故选：C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型：单选题

    在平面直角坐标系中，把点P（﹣3，2）绕原点O顺时针旋转180°，所得到的对应点P′的坐标为（ ）

    A. （3，2） B. （2，﹣3） C. （﹣3，﹣2） D. （3，﹣2）

    D 【解析】【解析】 根据题意得，点P关于原点的对称点是点P′，∵P点坐标为（-3，2）∴点P′的坐标（3，-2）．故选D．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册 22.3 二次函数的应用 同步测试 题型：单选题

    图（1）是一个横断面为抛物线形状的拱桥，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是（　　）

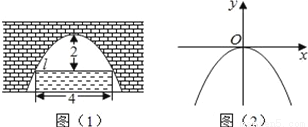
    A. y=﹣2x2 B. y=2x2 C. y=﹣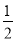x2 D. y=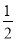x2

    C 【解析】试题分析：由图中可以看出，所求抛物线的顶点在原点，对称轴为y轴，可设此函数解析式为：y=ax2，利用待定系数法求解． 【解析】 设此函数解析式为：y=ax2，a≠0； 那么（2，﹣2）应在此函数解析式上． 则﹣2=4a 即得a=﹣， 那么y=﹣x2． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市2018届九年级上学期期中考试数学试卷 题型：填空题

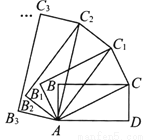
    （3分）如图，在矩形ABCD中，AD=2，CD=1，连接AC，以对角线AC为边，按逆时针方向作矩形ABCD的相似矩形AB1C1C，再连接AC1，以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1，．．．，按此规律继续下去，则矩形ABnCnCn-1的面积为 ．

    （或）． 【解析】 试题分析：AC===，因为矩形都相似，且每相邻两个矩形的相似比=，∴=2×1=2，=，===， ．．．，==．．．===． 故答案为：．

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市2018届九年级上学期期中考试数学试卷 题型：单选题

    小明同学将一张圆桌紧靠在矩形屋子的一角，与相邻两面墙相切，她把切点记为A、B，然后，她又在桌子边缘上任取一点P（异于A、B），则∠APB的度数为（ ）

    A. 45° B. 135° C. 45°或135° D. 90°或135°

    C 【解析】试题分析：连接OA、OB，则∠MAO=∠MBO=90°即可求得弧AB所对的圆心角的度数，然后分P在优弧和劣弧上两种情况进行讨论，利用圆周角定理即可求解． 【解析】 连接OA、OB，则∠MAO=∠MBO=90°， 又∵∠M=90°， ∴四边形AOBM是矩形。 ∴∠AOB=90°， 当P在AB所对的优弧上时，∠P=∠AOB=45°， 则当P在劣弧...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习（含解析） 题型：解答题

    抗洪救灾小组在甲地段有28人，乙地段有15人，现在又调来29人，分配在甲乙两个地段，要求调配后甲地段人数是乙地段人数的2倍，求应调至甲地段和乙地段各多少人？

    应调至甲地段20人，则调至乙地段9人 【解析】【解析】 设应调至甲地段x人，则调至乙地段（29-x）人-----1分 根据题意得 28+x=2（15+29-x） ------2分 解得 x=20 -------2分 经检验，符合题意 所以 29-x=9 ------1分 答：应调至甲地段20人，则调至乙地段9人 --------1分

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习（含解析） 题型：填空题

    小明与家人和同学一起到游泳池游泳，买了2张成人票与3张学生票，共付了155元．已知成人票的单价比学生票的单价贵15元，设学生票的单价为x元，可得方程______．

    3x＋2（x＋15）＝155 【解析】根据等量关系:2张成人票的价钱+3张学生票的价钱=共付的钱数,设学生票的单价为x元,因为成人票的单价比学生票的单价贵15元,所以成人票的单价为:(x+15)元,根据题意可列出方程为: 3x＋2（x＋15）＝155,故答案为: 3x＋2（x＋15）＝155.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 第23章小结与复习 测试 题型：解答题

    如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图．

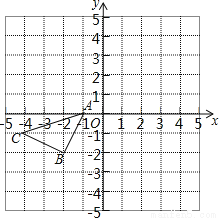
    （1）将△ABC向右平移1个单位长度，再向上平移4个单位长度，请画出平移后的△A1B1C1．

    （2）画出△ABC关于坐标原点O成中心对称的△A2B2C2．

    见解析 【解析】 试题分析：（1）直接利用平移的性质得出各点坐标，进而得出答案； （2）直接利用关于原点对称点的性质得出各点坐标，进而得出答案． 【解析】 （1）如图所示：△A1B1C1，即为所求； （2）如图所示：△A2B2C2，即为所求．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.3实际问题与二次函数（3）测试 题型：单选题

    心理学家发现，学生对概念的接受能力y与提出概念所用的时间x（单位：分）之间满足函数关系：y＝－0.1x2＋2.6x＋43 （0≤x≤30）．

    y值越大，表示接受能力越强．如果学生的接受能力逐步增强，则x的取值范围是（ ）

    A. 0≤x≤13 B. 13≤x≤26 C. 0≤x≤26 D. 13≤x≤30

    A 【解析】试题分析：对于开口向下的函数而言，对称轴的左边为增函数，对称轴的右边为减函数．本题中二次函数的对称轴为：直线x=13，则当时，y随着x的增大而增大，故选择A．

    查看答案和解析>>

    同步练习册答案