练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知二次函数y＝ax2＋bx＋c的图象如图，则下列叙述正确的是( )

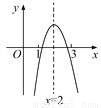
    A. abc＜0 B. －3a＋c＜0

    C. b2－4ac≥0 D. 将该函数图象向左平移2个单位后所得到抛物线的解析式为y＝ax2＋c

    B 【解析】解：A．由开口向下，可得a＜0；又由抛物线与y轴交于负半轴，可得c＜0，然后由对称轴在y轴右侧，得到b与a异号，则可得b＞0，故得abc＞0，故本选项错误； B．根据图知对称轴为直线x=2，即=2，得b=﹣4a，再根据图象知当x=1时，y=a+b+c=a﹣4a+c=﹣3a+c＜0，故本选项正确； C．由抛物线与x轴有两个交点，可得b2﹣4ac＞0，故本选项错误； ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：单选题

    如图，不能判定△AOB和△DOC相似的条件是（　　）

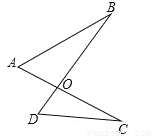
    A. AO•CO=BO•DO B. 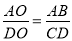C. ∠A=∠D D. ∠B=∠C

    B 【解析】选项A、能判定．利用两边成比例夹角相等． 选项B、不能判定． 选项C、能判定．利用两角对应相等的两个三角形相似． 选项D、能判定．利用两角对应相等的两个三角形相似． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测题 题型：填空题

    计算：()－1－＝____．

    0 【解析】原式=2-2=0. 故答案为：0.

    查看答案和解析>>

    科目：初中数学 来源：江西婺源县2016-2017学年九年级上期末考试数学试卷含答案 题型：解答题

    四张扑克牌（方块2、黑桃4、黑桃5、梅花5）的牌面如图l，将扑克牌洗匀后，如图2背面朝上放置在桌面上．小亮和小明设计的游戏规则是两人同时抽取一张扑克牌，两张牌面数字之和为奇数时，小亮获胜；否则小明获胜．请问这个游戏规则公平吗？并说明理由．

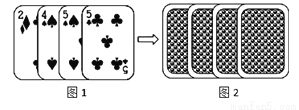
    不公平． 【解析】试题分析：先利用树状图展示所有有12种等可能的结果，其中两张牌面数字之和为奇数的有8种情况，再根据概率公式求出P（小亮获胜）和P（小明获胜），然后通过比较两概率的大小判断游戏的公平性． 试题解析：此游戏规则不公平．理由如下：画树状图得： 共有12种等可能的结果，其中两张牌面数字之和为奇数的有8种情况， 所以P(小亮获胜)= ；P(小明获胜)= ，因为＞，所...

    查看答案和解析>>

    科目：初中数学 来源：江西婺源县2016-2017学年九年级上期末考试数学试卷含答案 题型：填空题

    已知m，n是方程x2+2x﹣5=0的两个实数根，则m﹣mn +n =__________．

    3． 【解析】试题分析：根据题意得m+n=﹣2，mn=﹣5， 所以m+n﹣mn=2﹣（﹣5）=3．

    查看答案和解析>>

    科目：初中数学 来源：江西婺源县2016-2017学年九年级上期末考试数学试卷含答案 题型：单选题

    对于二次函数y=（x﹣1）2+2的图象，下列说法正确的是（　　）

    A. 开口向下 B. 对称轴是x=﹣1

    C. 顶点坐标是（1，2） D. 与x轴有两个交点

    C 【解析】试题分析：二次函数y=（x﹣1）2+2的图象开口向上，顶点坐标为（1，2），对称轴为直线x=1，抛物线与x轴没有公共点． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年八年级上学期第二次月考数学试卷 题型：解答题

    （1）化简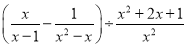： ，并从﹣1，0，1，2中选择一个合适的数求代数式的值．

    （2）已知x2＋y2＋6x－4y＋13=0，求 ．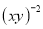

    （1）， ；（2）． 【解析】试题分析：（1）根据分式的混合运算的法则，通分，把除法化为乘法，完成约分化简，然后代入分母不为0的数（x≠±1，0）代入求值即可. （2）根据配方法和非负数的意义，直接变形，求出x、y的值，再代入求解即可. 试题解析：（1） = = = = 当x=2时，原式=. （2）∵x2＋y2＋6x－4y＋13=0 ∴x...

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年八年级上学期第二次月考数学试卷 题型：单选题

    已知x2+kxy+64y2是一个完全式，则k的值是（　　）

    A. 8 B. ±8 C. 16 D. ±16

    D 【解析】【解析】 ∵x2+kxy+16y2是一个完全平方式， ∴±2×x×4y=kxy， ∴k=±8． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2017-2018学年七年级上册数学期中联考试卷 题型：填空题

    若  ，则2x-y=________ ．

    13 【解析】根据非负数和相反数性质，可知2x-10=0，y+3=0，解得x=5，y=-3，代入2x-y=2×5-（-3）=13. 故答案为：13.

    查看答案和解析>>

    同步练习册答案