
若方程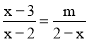 无解,则
无解,则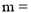 ______ .
______ .
科目:初中数学 来源:2017年甘肃省平凉市中考数学模拟试卷 题型:单选题
如图,已知正△ABC的边长为2,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数图象大致是( )
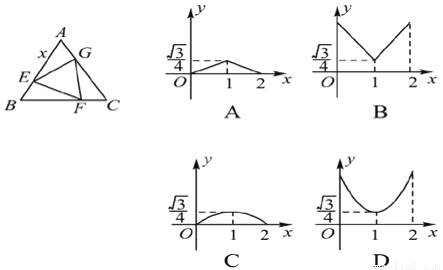
A. A B. B C. C D. D
D 【解析】试题分析:根据题意,有AE=BF=CG,且正三角形ABC的边长为2,故BE=CF=AG=2-x; 故△AEG、△BEF、△CFG三个三角形全等.在△AEG中,AE=x,AG=2-x, 则S△AEG=AE×AG×sinA=x(2-x); 故y=S△ABC-3S△AEG=-3x(2-x)=(3x 2-6x+4).故可得其图象为二次函数,且开口向上,查看答案和解析>>
科目:初中数学 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:解答题
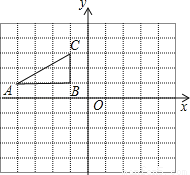
如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(﹣4,1),点B的坐标为(﹣1,1).
(1)先将Rt△ABC向右平移5个单位,再向下平移1个单位后得到Rt△A1B1C1.试在图中画出图形Rt△A1B1C1,并写出A1的坐标;
(2)将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出图形Rt△A2B2C2.并计算Rt△A1B1C1在上述旋转过程中C1所经过的路程.
查看答案和解析>>
科目:初中数学 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:单选题
下列说法正确的是( ).
A. “购买1张彩票就中奖”是不可能事件
B. “概率为0.0001的事件”是不可能事件
C. “任意画一个三角形,它的内角和等于180°”是必然事件
D. 任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
C 【解析】试题解析:A. “购买1张彩票就中奖”是不可能事件,错误; B. “概率为0.0001的事件”是不可能事件,错误; C. “任意画一个三角形,它的内角和等于180°”是必然事件,正确; D. 任意掷一枚质地均匀的硬币10次,正面向上的一定是5次,错误. 故选C.查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2017-2018学年八年级上学期八校联考数学试卷 题型:解答题
如图,点E在CD上,BC与AE交于点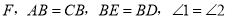 .
.
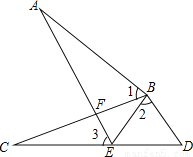
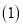 求证:
求证: 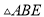 ≌
≌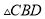 ;
;
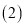 证明:
证明: 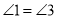 .
.
查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2017-2018学年八年级上学期八校联考数学试卷 题型:单选题
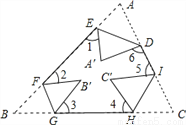
如图所示,把一个三角形纸片ABC的三个顶角向内折叠之后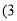 个顶点不重合
个顶点不重合 ,那么图中
,那么图中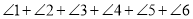 的度数和是
的度数和是
A. 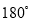
B. 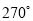
C. 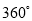
D. 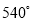
查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2017-2018学年八年级上学期八校联考数学试卷 题型:单选题
计算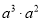 的结果是
的结果是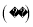
A. 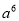 B.
B. 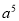 C.
C. 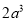 D. a
D. a
查看答案和解析>>
科目:初中数学 来源:江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型:填空题
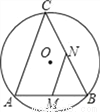
如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、BC的中点,则MN长的最大值是____________.
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:解答题
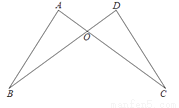
如图,AC与BD相交于点O,AO=DO,∠A=∠D.求证:△ABO≌△DCO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com