
已知a+2b=1,则2a+4b-3=______.
-1 【解析】利用整体思想,将所求式子变形后,将已知等式代入计算即可求出答案. 【解析】 ∵a+2b=1, ∴原式=2(a+2b)-3=2?3=-1. 故答案为:-1. 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第6章 反比例函数 单元测试卷 题型:单选题
下面的函数是反比例函数的是( )
A. y=3x-1 B. y=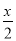 C. y=
C. y= D. y=
D. y=
查看答案和解析>>
科目:初中数学 来源:广西北海市银海区2017-2018学年度上期教学质量监测八年级数学试卷 题型:单选题
对于实数a、b,定义一种新运算“?”为:a?b=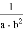 ,这里等式右边是实数运算.例如:1?3=
,这里等式右边是实数运算.例如:1?3=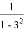 =
=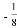 .则方程x?(﹣2)=
.则方程x?(﹣2)=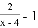 的解是( )
的解是( )
A. x=4 B. x=5 C. x=6 D. x=7
B 【解析】【解析】 根据题意,得,去分母得:1=2﹣(x﹣4),解得:x=5,经检验x=5是分式方程的解.故选B.查看答案和解析>>
科目:初中数学 来源:江苏省姜堰区2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
如图,是由一些棱长都为1的小正方体组合成的简单几何体.

(1)请画出这个几何体的三视图并用阴影表示出来;
(2)该几何体的表面积(含下底面)为 ;
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加 个小正方体.
(1)画图见解析;(2)28 ;(3)2. 【解析】试题分析:(1)根据主视图、左视图以及俯视图的观察角度,进而得出视图即可; (2)有顺序的计算上下面,左右面,前后面的表面积之和即可; (3)可在第二层第2列第一行加一个,第三层第2列第一行加一个,共2个. 试题解析:(1)如图所示: (2)(4×2+6×2+4×2)×(1×1) =(8+12+8)×1 ...查看答案和解析>>
科目:初中数学 来源:江苏省姜堰区2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
将一副三角板如图放置,若∠AOD=30°,则∠BOC=______.
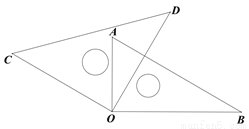
查看答案和解析>>
科目:初中数学 来源:江苏省姜堰区2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
下列各图中,可以是一个正方体的平面展开图的是( )
A. 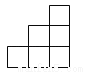 B.
B. 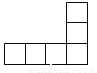 C.
C. 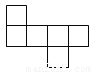 D.
D. 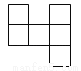
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第七章达标检测卷 题型:解答题
在平面直角坐标系中描出下列各点A(5,1),B(5,0),C(2,1),D(2,3),并顺次连接,且将所得图形向下平移4个单位,写出对应点A'、B'、C'、D'的坐标。
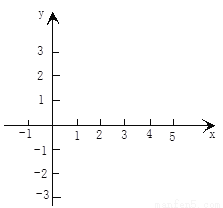
查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第2讲 整式与因式分解 题型:单选题
用棋子摆出下列一组图形(如图):

按照这种规律摆下去,第n个图形用的棋子个数为( )
A. 3n B. 6n
C. 3n+6 D. 3n+3
D 【解析】观察可知:①中有棋子6个,6=3×1+3, ②中有棋子9个,9=3×2+3, ③中有棋子12个,12=3×3+3, … 所以第n个图形用的棋子个数为:3n+3, 故答案为:3n+3.查看答案和解析>>
科目:初中数学 来源:河北省保定市莲池区2017-2018学年上期九年级数学期末考试试卷 题型:填空题
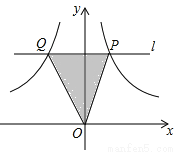
如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=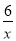 (x>0)和y=-
(x>0)和y=-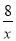 (x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .
(x<0)的图象交于点P、Q,连结PO、QO,则△POQ的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com