
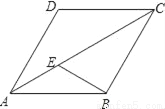
如图,在菱形ABCD中,E是对角线AC上一点,若AE=BE=2,AD=3,则CE=_____.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:北京八十五中2017-2018学年上期期末八年级数学试卷 题型:单选题
已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )
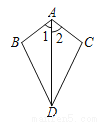
A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
B 【解析】试题分析:利用全等三角形判定定理ASA,SAS,AAS对各个选项逐一分析即可得出答案. 【解析】 A、∵∠1=∠2,AD为公共边,若AB=AC,则△ABD≌△ACD(SAS);故A不符合题意; B、∵∠1=∠2,AD为公共边,若BD=CD,不符合全等三角形判定定理,不能判定△ABD≌△ACD;故B符合题意; C、∵∠1=∠2,AD为公共边,若∠B=∠C,则△A...查看答案和解析>>
科目:初中数学 来源:2017年甘肃省平凉市中考数学模拟试卷 题型:解答题
如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=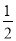 ,直线l上的点P位于y轴左侧,且到y轴的距离为1.
,直线l上的点P位于y轴左侧,且到y轴的距离为1.
(1)求直线l的表达式;
(2)若反比例函数 的图象经过点P,求m的值.
的图象经过点P,求m的值.

查看答案和解析>>
科目:初中数学 来源:2017年甘肃省平凉市中考数学模拟试卷 题型:单选题
我们身处在自然环境中,一年接受的宇宙射线及其它天然辐射照射量约为3100微西弗(1西弗等于1000毫西弗,1毫西弗等于1000微西弗),用科学记数法可表示为( )
A. 3.1×106西弗 B. 3.1×103西弗 C. 3.1×10﹣3西弗 D. 3.1×10﹣6西弗
C 【解析】3100微西弗=3.1毫西弗=3.1×10﹣3西弗.故选C.查看答案和解析>>
科目:初中数学 来源:2017年海南省定安县中考数学仿真试卷(二) 题型:解答题
如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:  ≈1.414,
≈1.414,  ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源:2017年海南省定安县中考数学仿真试卷(二) 题型:单选题
在一个不透明的袋中,装有2个红球和1个白球,这些球除颜色外其余都相同.搅均后从中随机一次摸出两个球,则两个球都是红球的概率是( )
A.  B.
B. 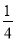 C.
C. 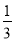 D.
D. 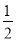
查看答案和解析>>
科目:初中数学 来源:2017年海南省定安县中考数学仿真试卷(二) 题型:单选题
2016年3月份我省农产品实现出口额8362万美元,其中8362万用科学记数法表示为( )
A. 8.362×107 B. 83.62×106 C. 0.8362×108 D. 8.362×108
A 【解析】由题意可得,8362万=8362 0000=8.362×107,故选A.查看答案和解析>>
科目:初中数学 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:填空题
已知二次函数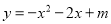 的部分图象如图所示,则一元二次方程
的部分图象如图所示,则一元二次方程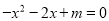 的解为:_____.
的解为:_____.
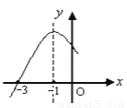
查看答案和解析>>
科目:初中数学 来源:江苏省东台市2017-2018学年上学期期末考试九年级数学试卷 题型:解答题
定义:如果一个数的平方等于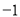 ,记为
,记为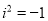 ,这个数
,这个数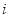 叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为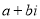 (
( 为实数),
为实数), 叫这个复数的实部,
叫这个复数的实部, 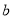 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算: 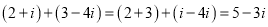
(1)填空: 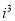 =_________,
=_________, 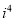 =____________.
=____________.
(2)填空:①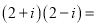 _________; ②
_________; ②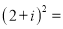 _________ .
_________ .
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, 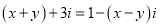 ,(
,( 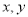 为实数),求
为实数),求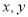 的值.
的值.
(4)试一试:请利用以前学习的有关知识将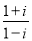 化简成
化简成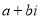 的形式.
的形式.
(5)解方程:x2 - 2x +4 = 0
(1) -I,1;(2)5,3+4i ;(3)x=-1,y=2;(4) i ;(5)x1= i ,x2= i 【解析】试题分析:(1)根据同底数幂的乘法法则、i2=﹣1计算即可; (2)利用平方差公式、完全平方公式把原式展开,根据i2=﹣1计算即可; (3)根据复数相等的条件解答即可; (4)充分利用i2=﹣1计算,分子分母同时乘以(1+i)即可; (5)计算出△=-...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com