
我们身处在自然环境中,一年接受的宇宙射线及其它天然辐射照射量约为3100微西弗(1西弗等于1000毫西弗,1毫西弗等于1000微西弗),用科学记数法可表示为( )
A. 3.1×106西弗 B. 3.1×103西弗 C. 3.1×10﹣3西弗 D. 3.1×10﹣6西弗
C 【解析】3100微西弗=3.1毫西弗=3.1×10﹣3西弗.故选C. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:北京八十五中2017-2018学年上期期末八年级数学试卷 题型:解答题
小鹏的家距离学校1600米,一天小鹏从家去上学,出发10分钟后,爸爸发现他的数学课本忘了拿,立即带上课本去追他,在学校门口追上了他,已知爸爸的速度是小鹏速度的2倍,求小鹏的速度.
小鹏的速度为80米/分. 【解析】试题分析:设小鹏的速度为x米/分,爸爸的速度为2x米/分,根据题意可得,走1600米爸爸比小鹏少用10分钟,据此列方程求解. 【解析】 设小鹏的速度为x米/分,爸爸的速度为2x米/分, 由题意得,﹣=10, 解得:x=80, 经检验,x=80是原分式方程的解,且符合题意. 答:小鹏的速度为80米/分.查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷 题型:单选题
下列运算正确的是( )
A. a+a=2a2 B. a2•a=2a2 C. (2a)2÷a=4a D. (﹣ab)2=ab2
C 【解析】A. ∵ a+a=2a,故不正确; B. ∵a2•a=a3 ,故不正确; C. ∵(2a)2÷a=4a,故正确; D. ∵(﹣ab)2=a2b2 ,故不正确; 故选C.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省平凉市中考数学模拟试卷 题型:填空题
为响应“书香成都”建设的号召,在全校形成良好的人文阅读风尚,成都市某中学随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中,阅读时间的中位数是________小时.
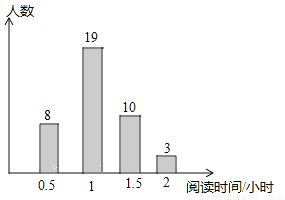
查看答案和解析>>
科目:初中数学 来源:2017年甘肃省平凉市中考数学模拟试卷 题型:单选题
如图AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )
的长为( )

A.  B.
B.  C.
C. 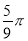 D.
D. 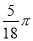
查看答案和解析>>
科目:初中数学 来源:2017年海南省定安县中考数学仿真试卷(二) 题型:解答题
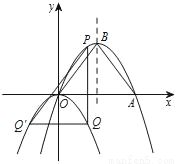
如图,抛物线y=﹣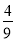 x2+bx+c经过原点和点A(6,0),与其对称轴交于点B,P是抛物线y=﹣
x2+bx+c经过原点和点A(6,0),与其对称轴交于点B,P是抛物线y=﹣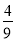 x2+bx+c上一动点,且在x轴上方.过点P作x轴的垂线交动抛物线y=﹣
x2+bx+c上一动点,且在x轴上方.过点P作x轴的垂线交动抛物线y=﹣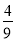 (x﹣h)2(h为常数)于点Q,过点Q作PQ的垂线交动抛物线y=﹣
(x﹣h)2(h为常数)于点Q,过点Q作PQ的垂线交动抛物线y=﹣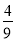 (x﹣h)2于点Q′(不与点Q重合),连结PQ′,设点P的横坐标为m.
(x﹣h)2于点Q′(不与点Q重合),连结PQ′,设点P的横坐标为m.
(1)求抛物线y=﹣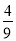 x2+bx+c的函数关系式及点B的坐标;
x2+bx+c的函数关系式及点B的坐标;
(2)当h=0时.
①求证: 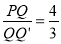 ;
;
②设△PQQ′与△OAB重叠部分图形的周长为l,求l与m之间的函数关系式;
(3)当h≠0时,是否存在点P,使四边形OAQQ′为菱形?若存在,请直接写出h的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017年海南省定安县中考数学仿真试卷(二) 题型:填空题
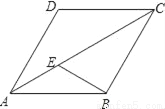
如图,在菱形ABCD中,E是对角线AC上一点,若AE=BE=2,AD=3,则CE=_____.
查看答案和解析>>
科目:初中数学 来源:重庆市校2018届九年级上学期期末模拟数学试卷 题型:解答题
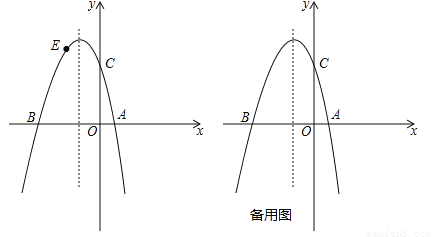
(14分)如图,已知抛物线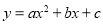 (
(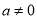 )与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
(1);(2)当a=时,S四边形BOCE最大,且最大值为,此时,点E坐标为(,);(3)P(﹣1,1)或(﹣1,﹣2). 【解析】 试题分析:(1)将A、B两点的坐标代入抛物线的解析式中,即可求出二次函数的解析式; (2)过E作EF⊥x轴于F.设E(a,)(﹣3<a<0),则EF=,BF=a+3,OF=﹣a,∴S四边形BOCE==BF•EF+(OC+EF)•OF =,配方即可得出...查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2017-2018学年八年级上学期八校联考数学试卷 题型:单选题
如图,每个图案都由若干个“●”组成,其中第 个图案中有7个“●”,第
个图案中有7个“●”,第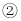 个图案中有13个“●”,则第
个图案中有13个“●”,则第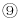 个图案中“●”的个数为
个图案中“●”的个数为
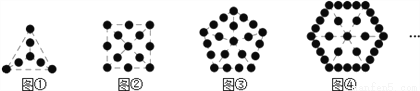
A. 57 B. 73 C. 91 D. 111
D 【解析】∵第个图案中“”有: 个, 第个图案中“”有: 个, 第个图案中“”有: 个, 第个图案中“”有: 个, ∴第个图案中“”有: 个, 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com