
把抛物线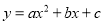 先向右平移3个单位,再向下平移2个单位,所得抛物线解析式为
先向右平移3个单位,再向下平移2个单位,所得抛物线解析式为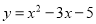 ,则a+b+c=___________。
,则a+b+c=___________。
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源:安徽省合肥市西校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
如图所示,l1反映了某公司产品的销售收入和销售数量的关系,l2反映产品的销售成本与销售数量的关系,根据图象判断公司盈利时的销售量为( )
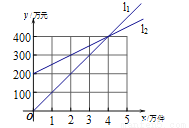
A. 小于4万件 B. 大于4万件
C. 等于4万件 D. 大于或等于4万件
B 【解析】两条直线交点为(4,400)也就是销售收入与销售成本相等,所以公司盈利需要大于4万件.选B.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.2.3关于原点对称的点的坐标 练习 题型:解答题
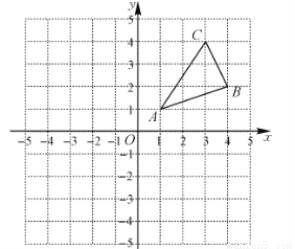
如图,△ABC三个顶点的坐标分别是A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
A、B、C向左平移5个单位后的坐标分别为(-4,1),(-1,2),(-2,4),连接这三个点,得△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB周长最小,请画出△PAB,并直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.2.3关于原点对称的点的坐标 练习 题型:填空题
已知点A的坐标为(-1,2),则点A关于x轴对称的点的坐标为____,关于y轴对称的点的坐标为____,关于原点对称的点的坐标为____.
(-1,-2), (1,2), (1,-2) 【解析】试题分析:两点关于x轴对称,则两个点的横坐标不变,纵坐标互为相反数;两点关于y轴对称,则两个点的横坐标互为相反数,纵坐标不变;两点关于原点对称,则两个点的横纵坐标都互为相反数.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:填空题
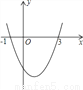
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有____________。
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:单选题
二次函数y=ax2+bx+c的图象如图所示,反比例函数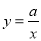 与正比例函数y=bx在同一坐标系内的大致图象是( )
与正比例函数y=bx在同一坐标系内的大致图象是( )
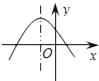
A. 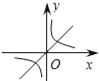 B.
B. 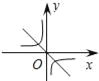 C.
C. 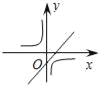 D.
D. 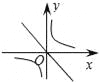
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:单选题
抛物线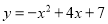 的顶点坐标为( )
的顶点坐标为( )
A. (-2,3) B. (2,11) C. (-2,7) D. (2,-3)
B 【解析】y=-x2+4x+7=-(x2-4x+4)+11=-(x-2)2+11, 故顶点坐标为(2,11). 故选B.查看答案和解析>>
科目:初中数学 来源:2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型:单选题
(2016黑龙江省牡丹江市)如图,在平面直角坐标系中,A(﹣8,﹣1),B(﹣6,﹣9),C(﹣2.﹣9),D(﹣4,﹣1).先将四边形ABCD沿x轴翻折,再向右平移8个单位长度,向下平移1个单位长度后,得到四边形A1B1C1D1,最后将四边形A1B1C1D1,绕着点A1旋转,使旋转后的四边形对角线的交点落在x轴上,则旋转后的四边形对角线的交点坐标为( )
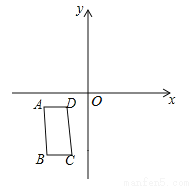
A. (4,0) B. (5,0) C. (4,0)或(﹣4,0) D. (5,0)或(﹣5,0)
D 【解析】【解析】 由题意得:A1(0,0),C1(6,8),根据四个点的坐标可知:四边形ABCD是平行四边形,∴对角线交点E1是A1C1的中点,∴E1(3,4),由勾股定理得:A1E1==5,当对角线交点落在x轴正半轴上时,对角线的交点坐标为(5,0),当对角线交点落在x轴负半轴上时,对角线的交点坐标为(﹣5,0),故选D.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(1)测试 题型:填空题
如图是两块完全一样的含30°角的直角三角尺,分别记做△ABC与△A′B′C′,现将两块三角尺重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角尺ABC,使其直角顶点C恰好落在三角尺A′B′C′的斜边A′B′上.当∠A=30°,AC=10时,两直角顶点C,C′间的距离是_____.
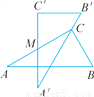
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com