练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    方程的根为__________．

    或 【解析】试题分析：x（x－2）=0，解得： =0， =2．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：内蒙古乌兰察布分校2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    据某统计数据显示，在我国的664座城市中，按水资源情况可分为三类：暂不缺水城市、一般缺水城市和严重缺水城市．其中，暂不缺水城市数比严重缺水城市数的4倍少50座，一般缺水城市数是严重缺水城市数的2倍．求严重缺水城市有多少座？

    102座. 【解析】试题分析：根据等量关系为：暂不缺水城市+一般缺水城市+严重缺水城市=664，据此列出方程，解可得答案． 【解析】 设严重缺水城市有x座， 依题意得：（3x+52）+x+2x=664． 解得：x=102． 答：严重缺水城市有102座．

    查看答案和解析>>

    科目：初中数学 来源：北京市海淀区2018届九年级上学期期末考试数学试卷 题型：填空题

    已知∠A为锐角，且tanA=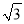，则∠A的大小为 _______________

    60° 【解析】∵∠A为锐角，且tanA=， ∴∠A=60°. 故答案为60.

    查看答案和解析>>

    科目：初中数学 来源：2018年1月北京市海淀区初三上数学期末试卷 题型：解答题

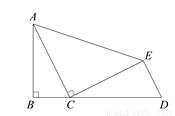
    如图，在△ABC中，∠B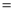90°，AB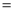4，BC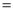2，以AC为边作△ACE，∠ACE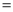90°，AC=CE，延长BC至点D，使CD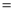5，连接DE．求证：△ABC∽△CED．

    证明见解析 【解析】试题分析： 由已知易证∠BAC=∠ECD，在Rt△ABC中由已知可得AC==CE， 结合AB=4，CD=5，可证得，由此即可由“两边对应成比例，且夹角相等的两三角形相似”得到△ABC∽△CED． 试题解析： ∵ ∠B=90°，AB=4，BC=2， ∴. ∵ CE=AC， ∴. ∵ CD=5， ∴. ∵ ∠B=90°，∠...

    查看答案和解析>>

    科目：初中数学 来源：2018年1月北京市海淀区初三上数学期末试卷 题型：填空题

    如图，AB是⊙O的直径，PA，PC分别与⊙O相切于点A，点C，若∠P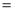60°，PA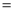 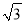，则AB的长为__________．

    2 【解析】∵AB是⊙O的直径，PA，PC分别与⊙O相切于点A，点C， ∴∠PAB=90°=∠ACB，PC=PA， 又∵∠P=60°， ∴△PAC是等边三角形， ∴∠CAP=60°，AC=PA=， ∴∠BAC=90°-60°=30°， ∴cos∠BAC=，即，解得AB=2. 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：2018年1月北京市海淀区初三上数学期末试卷 题型：单选题

    如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，则的大小为（　　）

    A. 30° B. 40° C. 50° D. 60°

    B 【解析】∵△ADE是由△ABC绕点A旋转100°得到的， ∴∠BAD=100°，AD=AB， ∵点D在BC的延长线上， ∴∠B=∠ADB=. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

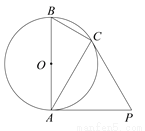
    如图，∠A=∠B，CE∥DA，CE交AB于E．求证：△CEB是等腰三角形．

    证明见试题解析． 【解析】 试题分析：由线的平行可得角相等，进行角的等量代换后再由两角相等确定等腰三角形． 试题解析：证明：∵CE∥DA，∴∠A=∠CEB．又∵∠A=∠B，∴∠CEB=∠B，∴CE=CB，∴△CEB是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源：云南省2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

    现有四根木棒，长度分别为4，6，8，10，从中任取三根木棒，能组成三角形的个数为（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】试题解析：共有4种方案： ①取4cm，6cm，8cm；由于8-4＜6＜8+4，能构成三角形； ②取4cm，8cm，10cm；由于10-4＜8＜10+4，能构成三角形； ③取4cm，6cm，10cm；由于6=10-4，不能构成三角形，此种情况不成立； ④取6cm，8cm，10cm；由于10-6＜8＜10+6，能构成三角形． 所以有3种方案符合要求． ...

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年第二学期无锡市惠山区初一数学期末试卷 题型：填空题

    分解因式：=___________．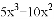

    5x2(x-2) 【解析】5x3-10x2=2x2(x-2)

    查看答案和解析>>

    同步练习册答案