
��ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ�Rt��ABC�Ķ�����ڸ���ϣ�����ƽ��ֱ������ϵ��A������Ϊ(-6��1)����B������Ϊ(-3��1)����C������Ϊ(-3��3)��
(1)��Rt��ABC��x��������ƽ��8����λ�õ�Rt��A1B1C1������ͼ�ϻ���Rt��A1B1C1����д����A1�����ꣻ
(2)��Rt��ABC�Ƶ�A˳ʱ����ת90��õ�Rt��A2B2C2������ͼ�ϻ���Rt��A2B2C2���������B������·����������������У�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ������
����33��52�䣫21��54�䣽__________________��������öȷ����ʾ��
55��46�� �����������������1��=60�䣮ԭʽ=54��106��=55��46�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʦ�����п���ѧ��ģ�Ծ� ���ͣ������
��ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=x+4��������ֱ���A��B���㣬������y=��x2+bx+c��A��B���㣬��DΪ�߶�AB��һ���㣬����D��CD��x���ڵ�C�����������ڵ�E��
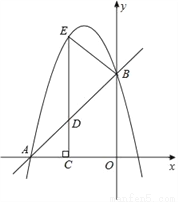
��1���������ߵĽ���ʽ��
��2�����ABE��������ֵ��
��3������BE���Ƿ���ڵ�D��ʹ�á�DBE�͡�DAC���ƣ������ڣ������D���ꣻ�������ڣ�˵�����ɣ�
��1��y=��x2��3x+4����2����ABE��������ֵΪ8����3�����ڵ�D��ʹ�á�DBE�͡�DAC���ƣ���D������Ϊ����3��1����2��2���� �������������������1�����������A��B�����꣬Ȼ�����ô���ϵ������������ߵĽ���ʽ�� ��2�����C����Ϊ��m��0����m��0�������E����Ϊ��m��-m2-3m+4�����Ӷ��ó�OC=-m��OF=-m2-3m+4��BF=-m2-3m������S��AB...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʦ�����п���ѧ��ģ�Ծ� ���ͣ���ѡ��
�����A��m��n����B��m��1��n��2������һ�κ���y=kx+b��k��0����ͼ���ϣ���ôk��ֵΪ��������
A. 2 B. 1 C. ��1 D. ��2
A ������������������ߵ�A��m��n����B��m-1��n-2������һ�κ���y=kx+b��k��0����ͼ���ϣ� �� ��ã�k=2�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������2017-2018��ʦ�����꼶���ϣ���ѧ��ĩģ���Ծ� ���ͣ������
�ס��������ۿ����72ǧ�ף�һ���ִ��Ӽ۳�����˳������3Сʱ�����Ҹۣ���Ϣ1Сʱ���������أ�һ�ҿ�ͧ���ִ�����2Сʱ����Ҹ۳�������������2Сʱ���ۣ����������أ���ͷʱ����Բ��ƣ�����֪ˮ���ٶ���2ǧ��/ʱ����ͼ��ʾ�ִ��Ϳ�ͧ��۵ľ���y��ǧ�ף����ִ�����ʱ��x��Сʱ��֮��ĺ�����ϵʽ�����ͼ�����������⣺
��˳���ٶ�=���ھ�ˮ���ٶȣ�ˮ���ٶȣ������ٶ�=���ھ�ˮ���ٶȣ�ˮ���ٶȣ�
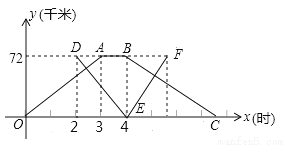
��1���ִ��ھ�ˮ�е��ٶ��� ǧ��/ʱ����ͧ�ھ�ˮ�е��ٶ��� ǧ��/ʱ��
��2�����ͧ����ʱ�Ľ���ʽ��д���Ա���ȡֵ��Χ��
��3����ͧ�����ʱ�䣬�ִ��Ϳ�ͧ�ڷ���;�����12ǧ�ף���ֱ��д�������
��1��22 �� 38��2��y=40x��160��4��x��5.8����3��3Сʱ��3.4Сʱ ���������������� ��1��22 �� 38�� ��2����F�ĺ�����Ϊ��4+72�£�38+2��=5.8 �� ��F��5.8��72����E��4��0���� ��EF����ʽΪy=kx+b��k��0������ ����á� ��y=40x��160��4��x��5.8���� ��3����ͧ����3Сʱ��3.4Сʱ�������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������2017-2018��ʦ�����꼶���ϣ���ѧ��ĩģ���Ծ� ���ͣ������
������x��y�Ķ�Ԫһ�η�����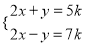 �Ľ����㷽��
�Ľ����㷽��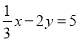 ����k=_________��
����k=_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������2017-2018��ʦ�����꼶���ϣ���ѧ��ĩģ���Ծ� ���ͣ���ѡ��
һ���ӵĿ��ȴ�����ȣ�Сǿ��Ӻӵ��ϰ����ε�����ȥ������ˮ��Ӱ�죬Сǿ�ϰ��ص�ƫ��Ŀ��ص�240m������ˮ��ʵ������510m����ô�úӵĿ���Ϊ�� ��
A. 450m B. 350m C. 270m D. 650m
A ��������������֪���ݣ����ù��ɶ����ӵĿ���==450�� ���ӵĿ���Ϊ450m�� ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�人���п���ѧģ���Ծ� ���ͣ������
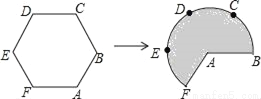
��ͼ�����߳�Ϊ3������������˿��ABCDEF����Ϊ�Ե�AΪԲ�ģ�ABΪ�뾶�����Σ�������˿�Ĵ�ϸ��������������AFB����Ӱ���֣������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ�����к���ѧУ2017-2018ѧ�����꼶�ϲ���ѧ���в��Ծ������𰸣� ���ͣ������
ͼ1�������ɸ�СԲȦ�ѳɵ�һ�������������ε�ͼ����������һ����һ��ԲȦ�����¸��������һ���һ��ԲȦ��һ������n�㣮��ͼ1���ú���ԭͼ1ƴ��ͼ2����״���������ǿ������ͼ1������ԲȦ�ĸ���Ϊ1+2+3+��+n=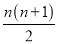 ��
��
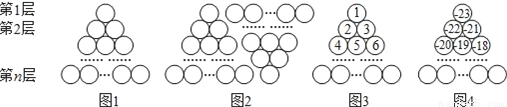
���ͼ1�е�ԲȦ����12�㣬
��1�������������£���ÿ��ԲȦ�ж���ͼ3�ķ�ʽ����һ��������������1��2��3��4����������ײ���������ԲȦ�е�����__��
��2�������������£���ÿ��ԲȦ�ж���ͼ4�ķ�ʽ����һ��������������23����22����21��������ͼ4������ԲȦ�и����ľ���ֵ֮�ͣ�
��1��67����2��1761�� �������������������1���������з������11���ԲȦ�����ټ�1���ɣ���2���������з������12���ԲȦ�����Ӷ�������23���������ж��ٸ��������ټ������ֵ�ĺ�. �������� ��1��11���ԲȦ��Ϊ=66�� ���12����������ԲȦ�е�����66+1=67�� ��2��ͼ4������ԲȦ�й���1+2+3+��+12==78����������23��������1��0��54...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com