
���ε��ܳ�Ϊ8cm����Ϊ1cm������������ڽǶ�����Ϊ��������
A. 3��1 B. 4��1 C. 5��1 D. 6��1
A �����������������������ѹ���⣮��Ҫ�����֪ʶ�㣺 ��1��ֱ���������У�30��������Ե�ֱ�DZߵ���б�ߵ�һ����涨���� ��2�����ε������ڽǻ����� ������֪��������εı߳����ٸ������Ǻ����������һ���ڽǴӶ��õ���һ���ڽǼ��ɵõ����������ڽǶ����ȣ� �������� ��ͼ��ʾ��������֪�ɵõ����εı߳�Ϊ2cm���Ӷ��ɵõ������ԵĽ�Ϊ30�㣬���ڵĽ�Ϊ150�㣬�������... ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ������
��ͼ����֪��AOB=90�㣬����OC�Ƶ�O��OAλ�ÿ�ʼ����ÿ��4����ٶ�˳ʱ�뷽����ת��ͬʱ������OD�Ƶ�O��OBλ�ÿ�ʼ����ÿ��1����ٶ���ʱ�뷽����ת����OC��OA��180��ʱ��OC��ODͬʱֹͣ��ת��
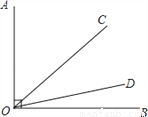
��1����OC��ת10��ʱ����COD=�� ���㣮
��2������תʱ��Ϊ�� ����ʱ��OC��OD�ļн���30�㣮
��3������תʱ��Ϊ�� ����ʱ��OBƽ�֡�CODʱ��
��1����COD=40�㣻��2��12��24����3��30. �������������������1��������ת���ٶȺ���ת��ʱ��ֱ������AOC�͡�BOD�Ķ�����Ȼ����ݡ�COD����AOB����AOC����BOD���ɼ���ó����ۣ� ��2����ת��t�룬OC��OD�ļн���30�ȣ�����ͼ1���з��̼��ɵõ����ۣ�����ͼ2���з��̼��ɵõ����ۣ� ��3����ͼ3����ת��m��ʱ�����ݽ�ƽ���ߵĶ����з��̼��ɵõ����ۣ� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
��ͼ��AB��CD��BP��CP�ֱ�ƽ�֡�ABC�͡�DCB��AD����P������AB��ֱ����AD��8�����P��BC�ľ����ǣ�������
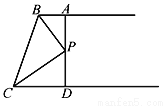
A. 8 B. 6 C. 4 D. 2
C ������������P��PE��BC��E�� ��AB��CD��PA��AB�� ��PD��CD�� ��BP��CP�ֱ�ƽ�֡�ABC�͡�DCB�� ��PA=PE��PD=PE�� ��PE=PA=PD�� ��PA+PD=AD=8�� ��PA=PD=4�� ��PE=4�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʦ�����п���ѧ��ģ�Ծ� ���ͣ������
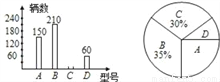
ij����С��Ϊ���˽�ijƷ�Ƶ綯���г��������������ijר�����һ���ȸ�Ʒ��A��B��C��D�����ͺŵ���������ͳ�ƣ����Ƴ���������ͳ��ͼ������������
��1���õ��һ�����۳�����Ʒ�Ƶĵ綯���г�����������
��2��������ͳ��ͼ����������
��3������ר����ƻ��������Ŀ��ͺŵĵ綯���г�1800������C�͵綯���г�Ӧ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʦ�����п���ѧ��ģ�Ծ� ���ͣ������
�̵�Ϊ�˶�ij����Ʒ������������Ϊ3Ԫ����Ʒ�������з�ʽ�Ż����ۣ���������5������ԭ�۸����һ���Թ���5�����ϣ��������ִ���ۣ������27ԪǮ�������Թ������Ʒ�ļ�����_____��
10 ���������������������Թ���x����������Ʒ�� 3��5+��x-5����3��0.8��27 ���x��10�� �������Թ������Ʒ�ļ�����10���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʦ�����п���ѧ��ģ�Ծ� ���ͣ���ѡ��
ij��2010��Ԫ����������������8�棬��������ǩ�2�棬�������������±�������¸ߣ�������
A. 10�� B. ��10�� C. 6�� D. ��6��
A �������������������������¼�ȥ������£��ٸ����������ļ������㷨��ȥһ�������ڼ�����������෴�����ã� 8-��-2��=8+2=10�森 ��ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ������2017-2018��ʦ�����꼶���ϣ���ѧ��ĩģ���Ծ� ���ͣ������
��֪x��yΪʵ������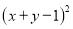 ��
��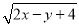 ��ֵ��Ϊ�෴������
��ֵ��Ϊ�෴������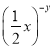 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�人���п���ѧģ���Ծ� ���ͣ������
��֪���κ���y=x2��2mx+4m��8,
��1����x��2ʱ������ֵy��x���������С����m��ȡֵ��Χ��
��2����������y=x2��2mx+4m��8�Ķ���AΪһ���������������ߵ��ڽ���������AMN��M��N�����ڒ������ϣ������ʣ���AMN���������m�صĶ�ֵ�����ǣ�����������ֵ�������ǣ���˵�����ɣ�
��3����������y=x2��2mx+4m��8��x�ύ��ĺ������Ϊ������������m����Сֵ��
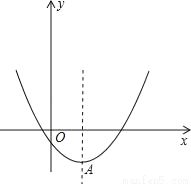
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017���㽭ʡ̨�����п���ѧ��ģ�Ծ� ���ͣ���ѡ��
��ͼ����ƽ���ı���ABCD�У�AC��BD�ཻ�ڵ�O��E��OD���е㣬����AE���ӳ���DC�ڵ�F����DF��FC=��������
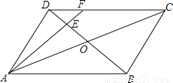
A. 1��4 B. 1��3 C. 1��2 D. 1��1
D �����������������⿼�����ƽ���ı��ε����ʺ����������ε��ж������ʶ���. ��������ƽ���ı���ABCD�У�AB��CD, �� ��ѡC.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com