
如图,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE剪开,剪下的三角形与原三角形相似的有( )
 (1) (2) (3) (4)
(1) (2) (3) (4)
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】 图1,∵∠CDE=∠B=70°, ∠C=∠C, ∴△CDE∽△CBA; 图2,∵∠CED=∠B=70°, ∠C=∠C, ∴△CDE∽△CAB; 图3,∵AC的长度不知道,∴无法说明 ,∴△ADE与△ABC不一定相似; 图4,∵∠BDE=∠A=70°, ∠BED=∠C, ∴△BDE∽△BAC; 故选C. 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:解答题
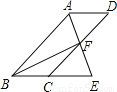
如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF平分∠ABE,EF=2,BF=4,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017届九年级上学期期末考试数学试卷 题型:填空题
据媒体报道,我国因环境污染造成的巨大经济损失,每年高达680000000元,这个数用科学记数法表示为______________元.
6.8×108 【解析】试题解析: 故答案为:查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:解答题
先化简,再求值: 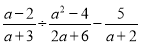 ,其中a=
,其中a=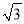 -2.
-2.
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:填空题
已知一组数据1,3,5,7,则该组数据的方差S2=_________.
5 【解析】, ∴.查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型:单选题
-2018的倒数是( )
A. 2018 B. 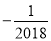 C.
C. 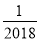 D. -2018
D. -2018
查看答案和解析>>
科目:初中数学 来源:浙江省2017学年第一学期七年级期末检测数学试卷卷 题型:解答题
化简:(1)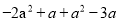 (2)
(2)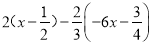
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
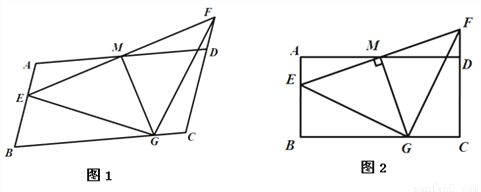
如图,在平行四边形ABCD中,AB=2,AD=4,M是AD的中点,点E是线段AB上一动点(可以运动到点A和点B),连接EM并延长交线段CD的延长线于点F.
(1) 如图1,①求证:AE=DF; ②若EM=3,∠FEA=45°,过点M作MG⊥EF交线段BC于点G,请直接写出△GEF的的形状,并求出点F到AB边的距离;
(2)改变平行四边形ABCD中∠B的度数,当∠B=90°时,可得到矩形ABCD(如图2),请判断△GEF的形状,并说明理由;
(3)在(2)的条件下,取MG中点P,连接EP,点P随着点E的运动而运动,当点E在线段AB上运动的过程中,请直接写出△EPG的面积S的范围.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市下城区安吉路良渚实验初三上期中数学试卷 题型:单选题
二次函数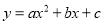 的图象,如图所示,有下列
的图象,如图所示,有下列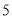 个结论:①
个结论:①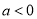 ;②
;②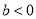 ;③
;③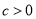 ;④
;④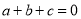 ;⑤
;⑤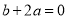 中,则其中正确的有( ).
中,则其中正确的有( ).
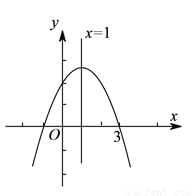
A. ①③④ B. ②④⑤ C. ①②④ D. ①③⑤
D 【解析】由函数图象可知:抛物线开口向下,∴a<0,故选项①正确; ∵对称轴在y轴右边,即x=?=1>0, 又a<0,∴b>0,故选项②错误; 又抛物线与y轴交点在y轴正半轴,∴c>0,故选项③正确; 当x=1时,对应的图象上的点在x轴上方,即y=ax2+bx+c=a+b+c>0,故选项④错误; 由x=?=1变形得:2a+b=0,故选项⑤正确; 综上,正...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com