
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
计算: 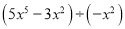 =____________.
=____________.
查看答案和解析>>
科目:初中数学 来源:北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型:解答题
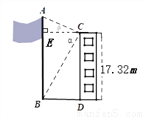
如图,建筑物的高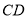 为17. 32米.在其楼顶
为17. 32米.在其楼顶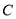 ,测得旗杆底部
,测得旗杆底部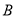 的俯角
的俯角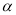 为
为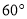 ,旗杆顶部
,旗杆顶部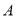 的仰角
的仰角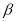 为
为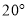 ,请你计算旗杆的高度.(
,请你计算旗杆的高度.(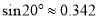 ,
, 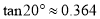 ,
, 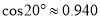 ,
,  ,结果精确到0.1米)
,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源:北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型:单选题
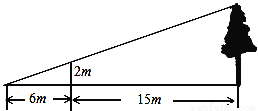
如图:为了测量某棵树的高度,小刚用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点距离6m,与树相距15m,那么这棵的高度为( )
A.5米 B.7米 C.7.5米 D .21米
A. 【解析】 试题解析:如图; AD=6m,AB=21m,DE=2m; 由于DE∥BC,所以△ADE∽△ABC,得: ,即, 解得:BC=7m, 故树的高度为7m. 故选A.查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:解答题
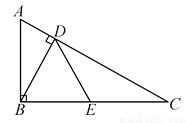
如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D ,点E为线段BC的中点,AD=2,tan A=2.
(1)求AB的长;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端25米的B处,测得树顶A的仰角∠ABO为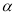 ,则树OA的高度为 ( )
,则树OA的高度为 ( )
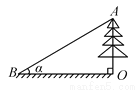
A. 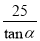 米 B. 25
米 B. 25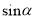 米 C. 25
米 C. 25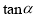 米 D. 25
米 D. 25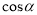 米
米
查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:单选题
顺次连结矩形各边中点所得的四边形是( ).
A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形
B. 【解析】 试题分析:作出图形,根据三角形的中位线定理可得EF=GH=AC,FG=EH=BD,再根据矩形的对角线相等可得AC=BD,从而得到四边形EFGH的四条边都相等,然后根据四条边都相等的四边形是菱形解答. 如图,连接AC、BD ∵E、F、G、H分别是矩形ABCD的AB、BC、CD、AD边上的中点, ∴EF=GH=AC,FG=EH=BD, ∵矩形ABCD...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
把一根长为120cm的木棍锯成两段,若使其中一段的长比另一段的2倍少3cm,则锯出的木棍的长不可能为( )
A. 80cm B. 41cm C. 79cm D. 41cm或79cm
C 【解析】试题解析:设一段为x,则另一段为(2x-3), 由题意得,x+2x-3=120, 解得:x=41(cm), 则另一段为:79(cm). 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:解答题
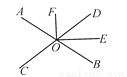
如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com