
把一根长为120cm的木棍锯成两段,若使其中一段的长比另一段的2倍少3cm,则锯出的木棍的长不可能为( )
A. 80cm B. 41cm C. 79cm D. 41cm或79cm
C 【解析】试题解析:设一段为x,则另一段为(2x-3), 由题意得,x+2x-3=120, 解得:x=41(cm), 则另一段为:79(cm). 故选C.科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年七年级上学期期末测评数学试卷 题型:单选题
下列说法不正确的是( )
A. 两点之间,直线最短 B. 两点确定一条直线
C. 互余两角度数的和等于90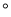 D. 同角的补角相等
D. 同角的补角相等
查看答案和解析>>
科目:初中数学 来源:海南省定安县2018届九年级上学期期末考试数学试卷 题型:填空题
计算: 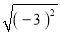 =_______.
=_______.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
如图,已知线段AB和CD的公共部分BD 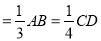 ,线段AB、CD的中点E、F之间的距离是25cm,试求AB、CD的长.
,线段AB、CD的中点E、F之间的距离是25cm,试求AB、CD的长.

查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
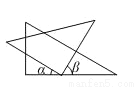
将一副三角板按如图所示放置摆放,已知∠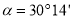 ,则∠
,则∠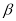 的度数是________.
的度数是________.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
下列说法正确的个数( )
①线段有两个端点,直线有一个端点;②点A到点B的距离就是线段AB;③两点之间线段最短;④ 若AB=BC,则点B为线段AC的中点;⑤同角(或等角)的余角相等.
A. 4个 B. 3个 C. 2个 D. 1个
C 【解析】试题解析:①线段有两个端点,直线没有端点,故①错误; ②点A到点B的距离就是线段AB的长度,故②错误; ③两点之间线段最短,正确; ④若AB=BC,点B在线段AC上时,则点B为线段AC的中点,故④错误; ⑤同角(或等角)的余角相等,正确. 故选C.查看答案和解析>>
科目:初中数学 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:解答题
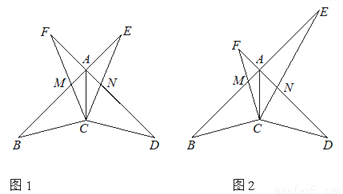
如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角的两边与BA,DA交于点M,N,与BA,DA的延长线交于点E,F,连接AC.
(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;
(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源:北京市丰台区2018届九年级第一学期期末数学试卷 题型:填空题
半径为2的圆中,60°的圆心角所对的弧的弧长为_____.
【解析】根据弧长公式可得: = , 故答案为: .查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级上学期期末考试数学试卷 题型:填空题
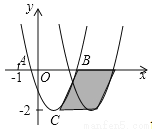
如图,已知抛物线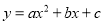 与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线
与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线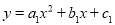 , 则下列结论:① a﹣b+c>0;②b>0;③阴影部分的面积为4;④若c=﹣1,则
, 则下列结论:① a﹣b+c>0;②b>0;③阴影部分的面积为4;④若c=﹣1,则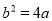 . 其中正确的是__________(写出所有正确结论的序号)
. 其中正确的是__________(写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com