
�ڡ�ABC�У���A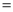 90�㣬AB
90�㣬AB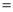 AC��
AC��
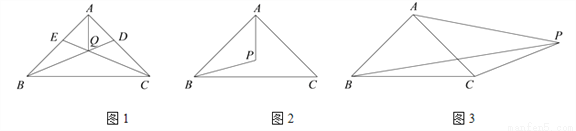
��1����ͼ1����ABC�Ľ�ƽ����BD��CE���ڵ�Q�����жϡ�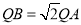 ���Ƿ���ȷ��________����ǡ�����
���Ƿ���ȷ��________����ǡ�����
��2����P�ǡ�ABC����ƽ���ڵ�һ�㣬����PA��PB����PB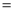
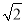 PA��
PA��
����ͼ2����P�ڡ�ABC�ڣ���ABP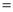 30�㣬���PAB�Ĵ�С��
30�㣬���PAB�Ĵ�С��
����ͼ3����P�ڡ�ABC�⣬����PC�����APC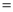 ������BPC
������BPC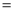 �£��õ�ʽ��ʾ������֮���������ϵ����֤����Ľ��ۣ�
�£��õ�ʽ��ʾ������֮���������ϵ����֤����Ľ��ۣ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�������з�̨��2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ���WORD�棩 ���ͣ������
���㣺12��20����4=______________��
49��20�� �����������������1��=60�䣬1��=60�壬��ԭʽ=48��80��=49��20�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹ������첼��У2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
 �ĵ�����
�ĵ�����
A. 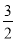 B.
B. 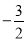 C.
C. 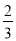 D.
D. 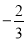
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������к�����2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
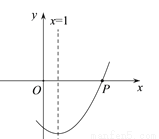
��ͼ��������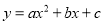 �ĶԳ���Ϊ
�ĶԳ���Ϊ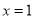 ����P����Q����������x����������㣬����P������Ϊ��4��0�������Q������Ϊ__________��
����P����Q����������x����������㣬����P������Ϊ��4��0�������Q������Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������к�����2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
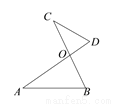
��ͼ����OAB�ס�OCD��OA��OC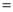 3��2����A
3��2����A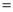 ������C
������C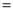 �£���OAB���OCD������ֱ���
�£���OAB���OCD������ֱ���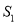 ��
��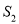 ����OAB���OCD���ܳ��ֱ���
����OAB���OCD���ܳ��ֱ���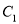 ��
��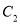 �������е�ʽһ���������ǣ�������
�������е�ʽһ���������ǣ�������
A. 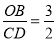 B.
B. 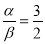 C.
C. 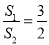 D.
D. 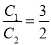
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018��1�±����к�������������ѧ��ĩ�Ծ� ���ͣ������
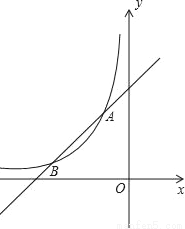
��ͼ������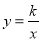 ��x��0����y=ax+b��ͼ���ڵ�A����1��n���͵�B����2��1����
��x��0����y=ax+b��ͼ���ڵ�A����1��n���͵�B����2��1����
��1����k��a��b��ֵ��
��2��ֱ��x=m��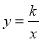 ��x��0����ͼ���ڵ�P����y=��x+1��ͼ���ڵ�Q������PAQ��90��ʱ��ֱ��д��m��ȡֵ��Χ��
��x��0����ͼ���ڵ�P����y=��x+1��ͼ���ڵ�Q������PAQ��90��ʱ��ֱ��д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018��1�±����к�������������ѧ��ĩ�Ծ� ���ͣ������
�����ǡ���һ��30��ǡ��ij߹���ͼ���̣�
��֪��ƽ����һ��A��
��������A��ʹ�á�A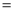 30�㣮
30�㣮
��������ͼ��
��1��������AB��
��2��������AB��ȡһ��O����OΪԲ�ģ�OAΪ�뾶��Բ��������AB�ཻ�ڵ�C��
 ��3����CΪԲ�ģ�OCΪ�뾶���������O���ڵ�D��������AD��
��3����CΪԲ�ģ�OCΪ�뾶���������O���ڵ�D��������AD��
��DAB��Ϊ����Ľǣ�
��ش𣺸ó߹���ͼ�������� ��
��������ȵ��������ǵȱ������Σ��ȱ������ε������ڽǶ���60�㣬һ�������Ե�Բ�ܽ���������Բ�Ľǵ�һ�룻 ��ֱ�����Ե�Բ�ܽ�Ϊֱ�ǣ���������ȵ��������ǵȱ������Σ��ȱ������ε������ڽǶ���60�㣬ֱ��������������ǻ��ࣻ ��ֱ�����Ե�Բ�ܽ�Ϊֱ�ǣ� �� Ϊ��ǣ� . ����������ͼ������OD��DC��������Ŀ����ͼ�����������������ַ���˵��������A=30�㣺 ��1����������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ��ʾ���ڡ�ABC�У�AD�ǽ�ƽ���ߣ�DE��AB�ڵ�E��DF��AC�ڵ�F��
��֤����1��AE=AF����2��DAƽ�֡�EDF��
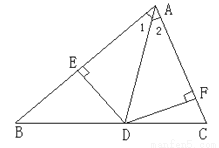
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2016-2017ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
���д����ҵı��Σ�������ʽ�ֽ���ǣ� ��
A. (x+1)(x-1)=x2-1 B. m2+m-4=(m+3)(m-2)+2 C. x2+2x=x(x+2) D. x2-5x+6=x(x-5) +6
C ��������������ʽ�ֽ�Ķ���֪ѡC.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com