练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一枚均匀的正方体骰子，六个面分别标有数字1、2、3、4、5、6，连续抛掷两次，朝上的数字分别是m、n，若把m、n作为点的横、纵坐标，那么点A（m，n）在函数y =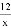 的图象上的概率是多少？

    【解析】试题分析：投掷两次，数目较多，可采用列表法求解．然后从表中找到m•n=12的数据占总数据的多少． 试题解析：【解析】 列表得： 可得，以（m，n）为坐标的点A共有36个，而只有（2，6），（3，4），（4，3），（6，2）四个点在函数的图象上，所以所求概率是=．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级上册数学 24.2.2直线和圆的位置关系（1）练习 题型：填空题

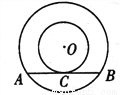
    如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆半径为10cm，小圆半径为6cm，则弦AB的长为_______cm．

    16 【解析】设切点是C，连接OA，OC．则在Rt△OAC中，AC==8cm，所以AB=16cm．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.1图形的旋转（2）测试 题型：填空题

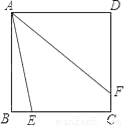
    如图，自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F，∠EAF=45°，在保持∠EAF=45°的前提下，当点E、F分别在边BC、CD上移动时，BE+DF与EF的关系是______．

    BE+DF=EF 【解析】如图,延长CD到M,使DM=BE, 连接AM,EF, ∵四边形ABCD为正方形, ∴∠B=∠ADC=90°,AB=AD, 在△ABE与△ADM中, , ∴△ABE≌△ADM（SAS）, ∴∠BAE=∠DAM,AE=AM, ∴∠BAE+∠DAF=∠DAM+∠DAF=∠MAF, ∵∠EAF=45°, ∴∠EAF...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.4弧长和扇形面积（2）练习 题型：填空题

    已知圆锥的母线与高的夹角为30°，母线长为4 cm，则它的侧面积为_________ cm2(结果保留π).

    8π 【解析】由题意知，底面半径是2，则底面周长是4π，所以侧面积是.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 24.4弧长和扇形面积（2）练习 题型：填空题

    已知Rt△ABC的两直角边AC=5 cm，BC=12 cm，则以BC为轴旋转所得的圆锥的侧面积为__________ cm2，这个圆锥的侧面展开图的弧长为__________ cm，面积为___________ cm2.

    65π 10π 65π 【解析】试题解析：如图， 在中， 这个圆锥的侧面积也就是这个圆锥的侧面展开扇形的面积. 因为侧面展开图的弧长等于底面圆的周长，所以侧面展开图的弧长 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：《概率的进一步认识》单元测试4 题型：解答题

    将下面事件的字母写在最能代表它的概率的点上．

    A．投掷一枚硬币时，得到一个正面．

    B．在一小时内，你步行可以走80千米．

    C．给你一个骰子中，你掷出一个3．

    D．明天太阳会升起来．

    见解析. 【解析】试题分析：根据概率公式和P（必然事件）=1；P（不可能事件）=0分别求出四个事件的概率，然后在图上分别标出即可． 试题解析：A.投掷一枚硬币时，得到一个正面的概率=； B.在一小时内，你步行可以走80千米的概率=0； C.给你一个骰子中，你掷出一个3的概率=； D.明天太阳会升起来的概率=1． 如图： ．

    查看答案和解析>>

    科目：初中数学 来源：《概率的进一步认识》单元测试4 题型：填空题

    某电视台综艺节目从接到的5000个热线电话中，抽取10名“幸运观众”，小颖打通了一次热线电话，她成为“幸运观众”的概率是________________.

    【解析】【解析】 因为共接到的5000个热线电话中，从中抽取10名“幸运观众”，小颖打通了一次热线电话，所以她成为“幸运观众”的概率是=．故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（2）测试 题型：解答题

    已知二次函数的图象如图所示，求此抛物线的解析式．

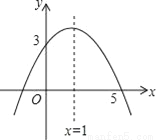
    y=﹣x2+x+3 【解析】试题分析：先利用抛物线的对称性确定抛物线与x轴的另一个交点坐标为（-3，0），则可设交点式为y=a（x+3）（x-5），然后把（0，3）代入求出a的值即可． 【解析】 ∵抛物线的对称轴为直线x=1， 而抛物线与x轴的一个交点坐标为（5，0）， ∴抛物线与x轴的另一个交点坐标为（﹣3，0） 设抛物线解析式为y=a（x+3）（x﹣5）， ...

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习（含答案） 题型：填空题

    如图，AB=AC，要使△ABE≌△ACD，依据ASA，应添加的一个条件是 ．

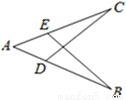
    ∠C=∠B． 【解析】 试题分析：此题主要考查了全等三角形的判定，关键是掌握判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL． 注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角． 可添加条件：∠B=∠C，再有条件AB=AC，∠A=∠A可利用ASA证明△ACD≌△ABE． 解...

    查看答案和解析>>

    同步练习册答案