练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

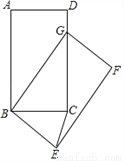
    如图，在矩形ABCD中，AB=5，BC=3，将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF，点A落在矩形ABCD的边CD上，连接CE，则CE的长是__________．

    【解析】【解析】 连接AG，由旋转变换的性质可知，∠ABG=∠CBE，BA=BG=5，BC=BE，由勾股定理得，CG==4，∴DG=DC﹣CG=1，则AG==，∵，∠ABG=∠CBE，∴△ABG∽△CBE，∴，解得，CE=，故答案为： ．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：单选题

    如图，从⊙O外一点P引⊙O的两条切线PA，PB，切点分别为A，B．如果∠APB=60°，PA=8，那么弦AB的长是（　　）

    A. 4 B. 8 C. 4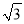 D. 8

    B 【解析】试题分析：∵PA,PB是圆O的两条切线，∴PA=PB. 又∵∠APB=60°，∴是等边三角形. 又∵PA=8，∴AB=8. 故选B.

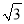
    查看答案和解析>>

    科目：初中数学 来源：山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型：解答题

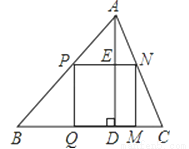
    如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成正方形零件PQMN，使正方形PQMN的边QM在BC上，其余两个项点P，N分别在AB，AC上．求这个正方形零件PQMN面积S．

    正方形零件PQMN面积是2304mm2. 【解析】试题分析：PN与AD交于点E，如图，设MN=xmm，则AE=AD﹣ED=80﹣x，再证明△APN∽△ABC，利用相似比可表示出PN=（80﹣x），根据正方形的性质得到（80﹣x）=x，然后结合正方形的面积公式进行解答即可． 试题解析：PN与AD交于点E，如图，设MN=xmm， 易得四边形MNED为矩形，则ED=MN=x， ∴...

    查看答案和解析>>

    科目：初中数学 来源：山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型：单选题

    抛物线y=x2－bx+8的顶点在x轴上，取b的值一定为(　　 )

    A. 4 B. -4 C. 2或-2 D. 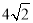或

    D 【解析】∵抛物线y=x2-bx+8的顶点在x轴上， ∴△=（-b)2-4×8=b2-32=0，解得b= ， 故选D．

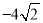
    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型：解答题

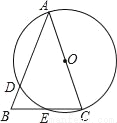
    如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．

    （1）求证：BE=CE；

    （2）若BD=2，BE=3，求AC的长．

    (1)证明见解析；（2）9. 【解析】试题分析：（1）连结AE，如图，根据圆周角定理，由AC为⊙O的直径得到∠AEC=90°，然后利用等腰三角形的性质即可得到BE=CE； （2）连结DE，如图，证明△BED∽△BAC，然后利用相似比可计算出AB的长，从而得到AC的长． 试题解析：（1）证明：连结AE，如图，∵AC为⊙O的直径，∴∠AEC=90°，∴AE⊥BC，而AB=AC，∴BE...

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型：解答题

    如图，抛物线y1=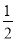（x+1）2+1与y2=a（x﹣4）2﹣3交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于B、C两点，且D、E分别为顶点．则下列结论：①a=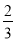；②AC=AE；③△ABD是等腰直角三角形；④当x＞1时，y1＞y2.其中正确结论的个数是（　 　）

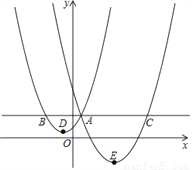
    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】【解析】 ∵抛物线与交于点A（1，3），∴3=a（1﹣4）2﹣3，解得：a=，故①正确； ∵E是抛物线的顶点，∴AE=EC，∴无法得出AC=AE，故②错误； 当y=3时，3=，解得：x1=1，x2=﹣3，故B（﹣3，3），D（﹣1，1），则AB=4，AD=BD=，∴AD2+BD2=AB2，∴③△ABD是等腰直角三角形，正确； ∵=时，解得：x1=1，x2=37...

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型：单选题

    在△ABC中，若|sinA﹣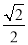|+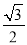（﹣cosB）2=0，∠A，∠B都是锐角，则∠C的度数是（　　）

    A. 75° B. 90° C. 105° D. 120°

    C 【解析】【解析】 ∵|sinA﹣|=0，（ ﹣cosB）2=0，∴sinA﹣=0， ﹣cosB=0，∴sinA=， =cosB，∴∠A=45°，∠B=30°，∴∠C=180°﹣∠A﹣∠B=105°．故选C．

    查看答案和解析>>

    科目：初中数学 来源：安徽省宿州市（城西校区） 2017-2018学年九年级第一学期期中测试数学试卷 题型：单选题

    为解决群众看病贵的问题，有关部门决定降低药价，对某种原价为289元的药品进行连续两次降价后为256元，设平均每次降价的百分率为x，则下面所列方程正确的是( )

    A. 289(1-x)2=256

    B. 256(1-x)2=289

    C. 289（1-2x)=256

    D. 256(1-2x)=289

    A 【解析】 试题分析：第一次降价后的价格为289(1-x)，第一次降价后的价格为289(1-x)（1-x),即289(1-x)2=256； 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版八年级数学下册 期末测评 题型：单选题

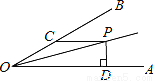
    如图，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，则PD的长为_____．

    2 【解析】试题分析：过P作PE⊥OB于E，根据角平分线的性质可得PE=PD，在求得∠BCP=30°，在Rt△ECP中，根据30°的锐角所对的直角边等于斜边的一半即可求得PD的长． 试题解析： 过P作PE⊥OB于E， ∵PD⊥OA，PE⊥OB，∠AOP=∠BOP=15°，∴∠BOA=30°，PE=PD， ∵PC∥OA，∴∠BOA=∠BCP=30°， 又△ECP为...

    查看答案和解析>>

    同步练习册答案