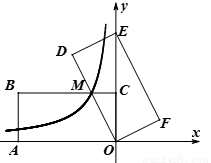
如图，在平面直角坐标系中，矩形OABC的顶点A、C分别在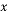
轴的负半轴、
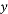轴的正半轴上，点B在第二象限.将矩形OABC绕点O顺时针旋转，使点B落在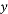轴上，得到矩形ODEF，BC与OD相交于点M.若经过点M的反比例函数y=
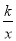（x＜0）的图象交AB于点N，的图象交AB于点N, S矩形OABC=32，tan∠DOE=
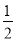,,则BN的长为______________.
考前必练系列答案科目：初中数学 来源：2017年初中毕业升学考试（贵州遵义卷）数学（解析版） 题型：解答题
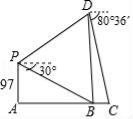
乌江快铁大桥是快铁渝黔线的一项重要工程，由主桥AB和引桥BC两部分组成（如图所示），建造前工程师用以下方式做了测量；无人机在A处正上方97m处的P点，测得B处的俯角为30°（当时C处被小山体阻挡无法观测），无人机飞行到B处正上方的D处时能看到C处，此时测得C处俯角为80°36′．
（1）求主桥AB的长度；
（2）若两观察点P、D的连线与水平方向的夹角为30°，求引桥BC的长．
（长度均精确到1m，参考数据：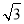
≈1.73，sin80°36′≈0.987，cos80°36′≈0.163，tan80°36′≈6.06）
查看答案和解析>>
科目：初中数学 来源：2017年初中毕业升学考试（贵州遵义卷）数学（解析版） 题型：选择题
我市连续7天的最高气温为：28°，27°，30°，33°，30°，30°，32°，这组数据的平均数和众数分别是（ ）
A．28°，30° B．30°，28° C．31°，30° D．30°，30°
查看答案和解析>>
科目：初中数学 来源：2017年初中毕业升学考试（湖北荆州卷）数学（解析版） 题型：解答题
已知关于x的一元二次方程x2+（k﹣5）x+1﹣k=0（其中k为常数）.
（1）求证无论k为何值，方程总有两个不相等实数根；
（2）已知函数y=x2+（k﹣5）x+1﹣k的图象不经过第三象限，求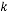
的取值范围；
（3）若原方程的一个根大于3，另一个根小于3，求k的最大整数值.
查看答案和解析>>
科目：初中数学 来源：2017年初中毕业升学考试（湖北荆州卷）数学（解析版） 题型：填空题
若关于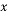
的分式方程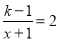
的解为负数，则k的取值范围为______________________.
查看答案和解析>>
科目：初中数学 来源：2017年初中毕业升学考试（湖北荆州卷）数学（解析版） 题型：选择题
如图，在△ABC中，AB=AC, ∠A =30°，AB的垂直平分线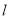
交AC于点D，则∠CBD的度数为（ ）
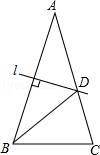
A.30° B.45° C.50° D.75°
查看答案和解析>>
科目：初中数学 来源：2017年初中毕业升学考试（湖北十堰卷）数学（解析版） 题型：填空题
如图，菱形ABCD中，AC交BD于O，OE⊥BC于E，连接OE，若∠ABC=140°，则∠OED= ．
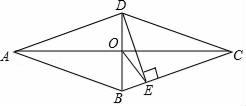
查看答案和解析>>
科目：初中数学 来源：2017年初中毕业升学考试（湖南益阳卷）数学（解析版） 题型：解答题
垫球是排球队常规训练的重要项目之一．下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩．测试规则为连续接球10个，每垫球到位1个记1分．
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩（分） | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
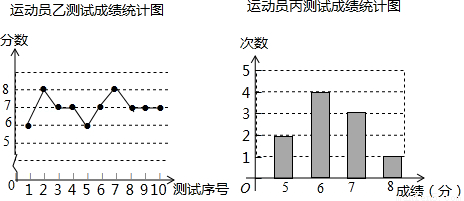
（1）写出运动员甲测试成绩的众数和中位数；
（2）在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适?为什么? (参考数据：三人成绩的方差分别为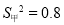
、
、
)
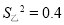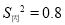（3）甲、乙、丙三人相互之间进行垫球练习，每个人的球都等可能的传给其他两人，球最先从甲手中传出，第三轮结束时球回到甲手中的概率是多少？（用树状图或列表法解答）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
B．
C．
D．