练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

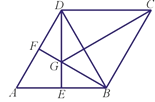
    如图，在菱形ABCD中，∠A=60°，E，F分别是AB，AD的中点，DE，BF相交于点G，连接BD，CG，有下列结论：①∠BGD=120° ；②BG+DG=CG；③△BDF≌△CGB；④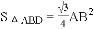．其中正确的结论有（ ）

    A. 1个 B. 2个 C. 3个 D. 4个

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省邵阳市2018年中考冲刺数学模拟试卷一 题型：填空题

    x是怎样的实数时，式子 在实数范围内有意义________ 。

    查看答案和解析>>

    科目：初中数学 来源：广东省2017-2018学年七年级6月月考数学试卷 题型：解答题

    如图，AB=AD，∠B=∠D．∠BAC=∠DAE, AC与AE相等吗？说说你的理由，

    查看答案和解析>>

    科目：初中数学 来源：安徽省桐城市2017-2018学年第二学期八年级期末学情检测 题型：解答题

    如图，在正方形ABCD中，点E在边AD上，点F在边BC的延长线上，连结EF与边CD相交于点G，连结BE与对角线AC相交于点H，AE=CF，BE=EG．

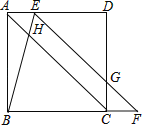
    （1）求证：EF∥AC；

    （2）求∠BEF大小；

    查看答案和解析>>

    科目：初中数学 来源：安徽省桐城市2017-2018学年第二学期八年级期末学情检测 题型：解答题

    计算

    查看答案和解析>>

    科目：初中数学 来源：安徽省桐城市2017-2018学年第二学期八年级期末学情检测 题型：单选题

    有下列的判断：

    ①△ABC中，如果a2＋b2≠c2，那么△ABC不是直角三角形

    ②△ABC中，如果a2－b2＝c2，那么△ABC是直角三角形

    ③如果△ABC 是直角三角形，那么a2＋b2＝c2

    以下说法正确的是（ ）

    A. ①② B. ②③ C. ①③ D. ②

    查看答案和解析>>

    科目：初中数学 来源：重庆市2017-2018学年八年级下学期期末第二次模拟考试数学试卷 题型：解答题

    阅读下面的情景对话，然后解答问题:

    老师:我们新定义一种三角形，两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.

    小明:那直角三角形是否存在奇异三角形呢？

    小红:等边三角形一定是奇异三角形.

    (1)根据“奇异三角形”的定义，小红得出命题：“等边三角形一定是奇异三角形”，则小红提出的命题是 .(填“真命题”或“假命题”)

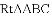
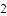
    (2)若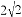是奇异三角形，其中两边的长分别为、，则第三边的长为 .

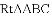
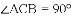
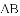
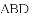
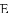
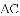
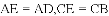
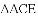
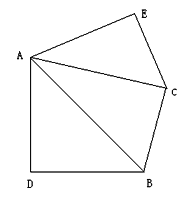
    (3)如图，中，,以为斜边作等腰直角三角形,点是上方的一点，且满足.求证:是奇异三角形．

    查看答案和解析>>

    科目：初中数学 来源：重庆市2017-2018学年八年级下学期期末第二次模拟考试数学试卷 题型：单选题

    下列条件中，能判定四边形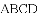为平行四边形的是( )

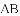
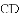
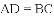
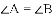
    A. ∥， B. ，

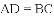
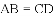
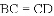
    C. ， D. ，

    查看答案和解析>>

    科目：初中数学 来源：安徽省2017-2018学年度下期八年级期末考试数学试卷 题型：解答题

    已知a，b是直角三角形的两边，且满足，求此三角形第三边长.

    查看答案和解析>>

    同步练习册答案