
���ж����У�û���涨�����ǣ� ����
A. ȫ�������ζ�Ӧ����� B. �߶δ�ֱƽ�����ϵĵ㵽�߶����˵ľ������
C. һ���������У��ȽǶԵȱ� D. ��ֱ��ƽ�У�ͬλ�����
A ��������Aѡ���У���Ϊ����Ӧ����Ȳ�һ����ȫ�������Ρ�������A�ж���û�����涨���� Bѡ���У���Ϊ�����߶����˾�����ȵĵ����߶εĴ�ֱƽ�����ϡ�������B�ж������涨���� Cѡ���У���Ϊ����ͬһ���������У��ȱ߶ԵȽǡ�������C�ж������涨���� Dѡ���У���Ϊ��ͬλ����ȣ���ֱ��ƽ�С�������D�ж������涨���� ��ѡA�� ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�괺��ʦ������꼶��ѧ�²��ҳ���Ծ�����ĩ���� ���ͣ���ѡ��
����ÿ�����ֱ�������Сľ���ij���, �����ܰڳ������ε��ǣ� ��
A��5, 1, 3 B��2, 4, 2 C��3, 3, 7 D��2, 3, 4
D ��������A��3+1��5�����ܹ��������Σ��ʱ�ѡ����� B��2+2=4�����ܹ��������Σ��ʱ�ѡ����� C��3+3��7�����ܹ��������Σ��ʱ�ѡ����� D��2+3��4���ܹ��������Σ��ʱ�ѡ����ȷ�� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
ijУ�ĸ��̻�С��ij���ֲ���������£�10��10��x��8�����������ݵ�������ƽ������ȣ���ô�������ݵ���λ���ǣ�������
A. 9 B. 10 C. 11 D. 12
B �������������������x=8ʱ����������������ƽ����ֻ��һ��������������ȥ. ������Ϊ10,��������� ���x=12�� ���������ݴ�С�����˳������8��10��10��12�� �����м�λ�õ���10��10�� �����������ݵ���λ����(10+10)��2=10. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����³���������ѧ2017-2018ѧ����꼶��ѧ���п�����ѧ�Ծ����������� ���ͣ������
��ͼ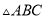 ��
��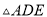 ������
������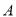 Ϊֱ�Ƕ���ĵ���ֱ�������Σ�
Ϊֱ�Ƕ���ĵ���ֱ�������Σ� 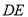 ��
��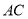 �ڵ�
�ڵ�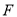 ����
����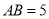 ��
��  ����
����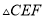 ��ֱ��������ʱ����
��ֱ��������ʱ���� �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�����³���������ѧ2017-2018ѧ����꼶��ѧ���п�����ѧ�Ծ����������� ���ͣ���ѡ��
��ͼ���������ζ��ۺ�չ����ͼ�����������ζ��ۺ���չ�������ٰ�ͼʾ�����۵����ܹ��õ�һ��ֱ�������Σ���Ӱ���֣���������һ��ֱ�DZߵ���б�ߵ�һ�룬������ͼ���У� ����

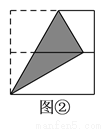


A. 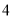 �� B.
�� B. 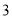 �� C.
�� C. 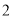 �� D.
�� D. 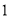 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ����2017-2018ѧ����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ������
��ͼ����һ��Բ��������Բ��ֱ��EF=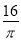 ����FC=12cm��PΪFC���е㣬�����ϴ�E������P�����̾����Ƕ��٣�������ƽ��ͼ�Σ�
����FC=12cm��PΪFC���е㣬�����ϴ�E������P�����̾����Ƕ��٣�������ƽ��ͼ�Σ�
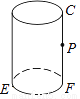
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ����2017-2018ѧ����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ������
��Rt��ABC�У���ACB=90�㣬AB=5cm��BC=3cm��CD��AB��D��CD= ________
cm ���������ȸ��ݹ��ɶ������ֱ�DZ�AC AC==4cm�������������ε����S��ABC=AC•CB=AB•CD��������� CD=cm�� �ʴ�Ϊ�� cm ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ1��������y= 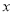 2+b
2+b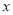 +c��x�ύ��A��-1,0����B��3��0�����㣬��y�ύ�ڵ�C.
+c��x�ύ��A��-1,0����B��3��0�����㣬��y�ύ�ڵ�C.
��1����������ߵĽ���ʽ��
��2����M�������ߵĶԳ�����ֱ��BC�Ľ��㣬N�������ߵĶ��㣬��MN�ij���
��3�����P�ǣ�1���е������ߵ�һ�����㣬�Ƿ��������S��PAB=8�ĵ�P������������P�����ꣻ�������ڣ���˵������.
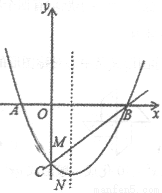
ͼ1 ����ͼ
��1��y=x2��2x��3����2��1����3����P�������ֱ�Ϊ��1+2��4������1��2��4������1����4��ʱ��S��PAB=8�� �������������������1���ѵ�A��B������ֱ���뺯������ʽ���г�����ϵ��b��c�ķ����飬ͨ���ⷽ����������ǵ�ֵ���ɣ� ��2����������ߵĽ���ʽ�õ���C��N�����꣬����B��C������������ֱ��BC�Ľ���ʽ����һ�κ���ͼ���ϵ�����������͵��������ͼ�ε����ʽ��н�...�鿴�𰸺ͽ���>>
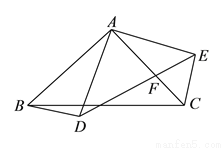
��Ŀ��������ѧ ��Դ������ʡ����������У2017-2018ѧ����꼶��ѧ������������ѧ�Ծ� ���ͣ������
��ͼ����֪��ABC�У�AB=AC=6cm��BC=4cm����DΪAB���е㣮
�������P���߶�BC����1cm/s���ٶ��ɵ�B���C�˶���ͬʱ����Q���߶�CA���ɵ�C���A�˶���
������Q���˶��ٶ����P���˶��ٶ���ȣ�����1���BPD���CPQ�Ƿ�ȫ�ȣ���˵�����ɣ�
������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ______cm/sʱ����ijһʱ��Ҳ�ܹ�ʹ��BPD���CPQȫ�ȣ�
������Q�Ԣ��е��˶��ٶȴӵ�C��������P��ԭ�����˶��ٶȴӵ�Bͬʱ������������ʱ�뷽���ء�ABC�������˶������������P���Q��һ����������д����һ���������ڡ�ABC���������ϣ�
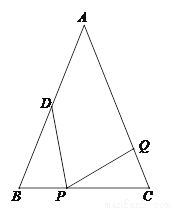
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com