练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

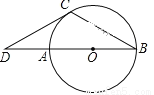
    已知：如图，AB是⊙O的直径，BC是弦，∠B=30°，延长BA到D，使∠BDC=30°．

    (1)求证：DC是⊙O的切线；

    (2)若AB=2，求DC的长．

    （1）证明见解析；（2）. 【解析】试题分析：（1）根据切线的判定方法，只需证CD⊥OC．所以连接OC，证∠OCD=90°； （2）易求半径OC的长．在Rt△OCD中，运用三角函数求CD． 试题解析：（1）连接OC． ∵OB=OC，∠B=30°， ∴∠OCB=∠B=30°， ∴∠COD=∠B+∠OCB=60°， ∵∠BDC=30°， ∴∠BDC+∠C...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年内蒙古包头市八年级（下）期中数学试卷 题型：填空题

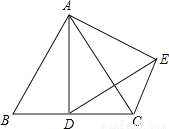
    如图，在等边△ABC中，AB=6，D是BC的中点，将△ABD绕点A旋转后得到△ACE，那么线段DE的长度为 ．

    3． 【解析】 试题分析：首先，利用等边三角形的性质求得AD=；然后根据旋转的性质、等边三角形的性质推知△ADE为等边三角形，则DE=AD． 试题解析：如图，∵在等边△ABC中，∠B=60°，AB=6，D是BC的中点， ∴AD⊥BD，∠BAD=∠CAD=30°， ∴AD=ABcos30°=6×=3． 根据旋转的性质知，∠EAC=∠DAB=30°，AD=AE， ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型：解答题

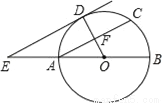
    如图，AB为⊙O的直径，F为弦AC的中点，连接OF并延长交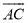于点D，过点D作⊙O的切线，交BA的延长线于点E．

    （1）求证：AC∥DE；

    （2）连接CD，若OA=AE=1，求四边形ACDE面积．

    （1）证明见解析；（2） 【解析】（1）欲证明AC∥DE，只要证明AC⊥OD，ED⊥OD即可． （2）作DM⊥OA于M，连接CD，CO，AD，首先证明四边形ACDE是平行四边形，根据S平行四边形ACDE=AE•DM，只要求出DM即可． （1）证明：∵ED与⊙O相切于D，∴OD⊥DE， ∵F为弦AC中点，∴OD⊥AC，∴AC∥DE． （2）【解析】 作DM⊥OA于M，...

    查看答案和解析>>

    科目：初中数学 来源：江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型：填空题

    方程x2 = 3x的解是_______________.

    0,3 【解析】∵x2 = 3x， ∴x2 - 3x=0， ∴x(x-3)=0 ∴x1=0,x2=3.

    查看答案和解析>>

    科目：初中数学 来源：江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型：单选题

    用配方法解方程x2＋4x＋3=0时，配方后得到的方程为（　　）

    A. (x＋2)2 = 1 B. ( x＋2)2 =3 C. (x－2)2 = 3 D. ( x－2)2 = 1

    A 【解析】∵x2＋4x＋3=0， ∴x2＋4x+4＋3=4， ∴(x+2)2=1. 选选A.

    查看答案和解析>>

    科目：初中数学 来源：河南省2018届九年级上学期期末考试数学试卷 题型：填空题

    第一盒乒乓球中有4个白球2个黄球，第二盒乒乓球中有3个白球3个黄球，分别从每个盒子中随机地取出1个球，则取出的两个球都是黄球的概率是______．

    【解析】第一个盒子里取出黄球概率是=，第二个盒子取出黄球, 取出的两个球都是黄球的概率是. 故答案为

    查看答案和解析>>

    科目：初中数学 来源：河南省2018届九年级上学期期末考试数学试卷 题型：单选题

    将抛物线y=﹣3x2平移，得到抛物线y=﹣3 （x﹣1）2﹣2，下列平移方式中，正确的是（　　）

    A. 先向左平移1个单位，再向上平移2个单位

    B. 先向左平移1个单位，再向下平移2个单位

    C. 先向右平移1个单位，再向上平移2个单位

    D. 先向右平移1个单位，再向下平移2个单位

    D 【解析】将抛物线y=-3x2平移，先向右平移1个单位得到抛物线y=-3（x-1）2, 再向下平移2个单位得到抛物线y=-3（x-1）2-2. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：内蒙古赤峰市翁牛特旗2018届九年级上学期期末考试数学试卷 题型：填空题

    把3x2－12x＋12因式分解的结果是____________________________．

    3（x-2）2 【解析】【解析】 原式==．故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：湖北省元月联合测试数学试卷 题型：解答题

    某商品现在售价为每件60元，每星期可卖出300件，市场调查反映：调整价格，每件涨价1元，每星期要少卖出10件；每件降价1元，每星期可多卖出20件.已知商品的进价为每件40元.

    （1）设每件降价x元，每星期的销售利润为y元；

    ① 请写出y与x之间的函数关系式；

    ② 确定x的值，使利润最大，并求出最大利润；

    （2）若涨价x元，则x= 元时，利润y的最大值为 元（直接写出答案，不必写过程）.

    （1）①②x=2或3时y最大为6120；（2）5， 6250 【解析】试题分析：（1）①设每件降价x元，每星期的销售利润为y元，根据等量关系“总利润=每件的利润×每星期的销售量”，写出函数关系式即可；②把函数的解析式化为顶点式，然后根据x取整数，即可求得最大利润；（2）表示出商品的周销售量，根据等量关系“总利润=每件的利润×每星期的销售量”，写出函数关系式，再根据二次函数的性质求出最大利润即...

    查看答案和解析>>

    同步练习册答案