
方程x2 = 3x的解是_______________.
0,3 【解析】∵x2 = 3x, ∴x2 - 3x=0, ∴x(x-3)=0 ∴x1=0,x2=3.科目:初中数学 来源:广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型:单选题
用配方法解一元二次方程x2+4x﹣3=0时,原方程可变形为( )
A. (x+2)2=1 B. (x+2)2=7 C. (x+2)2=13 D. (x+2)2=19
B 【解析】x2+4x﹣3=0, ∵x2+4x=3, ∴x2+4x+4=3+4,即(x+2)2=7, 故选:B.查看答案和解析>>
科目:初中数学 来源:江西婺源县2016-2017学年第一学期期末考试九年级数学试卷 题型:填空题
将抛物线y=x2向左平移5个单位,得到的抛物线解析式为_____________.
y=(x+5)2(或y=x2+10x+25). 【解析】根据抛物线的平移规律“左加右减,上加下减”可得将抛物线y=x2向左平移5个单位,得到的抛物线解析式为y=(x+5)2.查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型:解答题
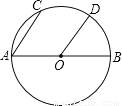
如图,已知AB是⊙O的直径,弦AC∥OD.
(1)求证: 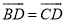 .
.
(2)若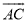 的度数为58 º,求∠AOD的度数.
的度数为58 º,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型:填空题
正六边形ABCDEF的半径为4,则此正六边形的面积为_________.
【解析】如图, 由题意得 ∠COD=360°÷ 6=60°, 又∵OC=OD, ∴ ∠GOD=30°, ∴Rt △DOG中:OD=4,GD= 4÷2 =2, ∴ ,CD=2GD=2×2=4, ∴△DOC的面积= , ∴正六边形ABCDEF的面积= .查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型:单选题
下列关于x的一元二次方程有实数根的是( )
A. x2 +1=0 B. x2+x-1= 0 C. 2x2 -2x+1= 0 D. 2x2 -3x+4= 0
B 【解析】A. ∵△=02-4×1×1=-4<0,∴ x2 +1=0没有实数根; B. ∵△=12-4×1×(-1)=5>0,∴ x2+x-1= 0有实数根; C. ∵△=(-2)2-4×2×1=-4<0,∴2x2 -2x+1= 0没有实数根; D. ∵△=(-3)2-4×2×4=-23<0,∴2x2 -3x+4= 0没有实数根; 故选B.查看答案和解析>>
科目:初中数学 来源:河南省2018届九年级上学期期末考试数学试卷 题型:解答题
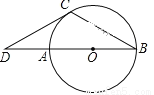
已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
查看答案和解析>>
科目:初中数学 来源:河南省2018届九年级上学期期末考试数学试卷 题型:单选题
若一元二次方程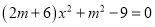 的常数项是0,则m等于
的常数项是0,则m等于
A. -3 B. 3 C. ±3 D. 9
B 【解析】,2m-6解得m=3.故选 B.查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:单选题
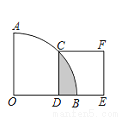
如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为1,则图中阴影部分的面积为( )
A. 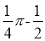 B.
B. 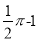 C.
C. 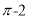 D.
D. 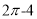
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com