练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若规定两数a、b通过“※”运算，得到4ab，即a※b=4ab，例如2※6=4×2×6=48

    （1）求3※5的值；

    （2）求x※x+2※x-2※4=0中x的值；

    （3）若无论x是什么数，总有a※x=x，求a的值．

    (1) x1=2，x2=-4;(2) x1=2，x2=-4;(3) 【解析】试题分析：要注意a※b=4ab新定义的运算方法，把已知数按照运算法则代入即可求值，后两问将数值代入后得到了两个方程，解方程即可． 试题解析：【解析】 （1）∵a※b=4ab，∴3※5=4×3×5=60； （2）由x※x+2※x﹣2※4=0得，4x2+8x﹣32=0，即x2+2x﹣8=0，∴x1=2，x2...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版初中数学七年级下册第五章《相交线与平行线--垂线》同步练习 题型：填空题

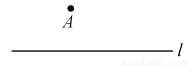
    如图，过直线l外一点A，作直线l的垂线，可以作__________条.

    1 【解析】试题解析：过直线l外一点A，作直线l的垂线，可以作1条. 故答案为：1.

    查看答案和解析>>

    科目：初中数学 来源：2018届中考数学专题复习同步练习题：一次函数 题型：填空题

    在平面直角坐标系中，已知一次函数y=2x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1 ______ y2．（填“＞”“＜”或“=”）

    ＜ 【解析】试题解析：∵一次函数y=2x+1中k=2＞0， ∴y随x的增大而增大， ∵x1＜x2， ∴y1＜y2．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年人教版七年级数学第五章相交线与平行线单元测试 题型：填空题

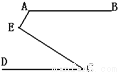
    如图，AB∥CD，∠BAE = 120º，∠DCE = 30º，则∠AEC = _______度.

    90° 【解析】【解析】 如图，延长AE交CD于点F， ∵AB∥CD， ∴∠BAE+∠EFC=180°． 又∵∠BAE=120°， ∴∠EFC=180°-∠BAE=180°-120°=60°， 又∵∠DCE=35°， ∴∠AEC=∠DCE+∠EFC=30°+60°=90°． 故答案为90．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年人教版七年级数学第五章相交线与平行线单元测试 题型：单选题

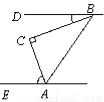
    如图，在△ABC 中，∠C＝90°．若BD∥AE，∠DBC＝20°，则∠CAE的度数是 （ ）

    A．40°   B．60° C．70° D．80°

    C 【解析】 试题分析：过点C作CF∥BD，根据两直线平行，内错角相等即可求解。 【解析】 过点C作CF∥BD，则CF∥BD∥AE． ∴∠BCF=∠DBC=20°， ∵∠C=90°， ∴∠FCA=90°-20°=70°． ∵CF∥AE， ∴∠CAE=∠FCA=70°．

    查看答案和解析>>

    科目：初中数学 来源：人教版初中数学九年级上册第二十一章《配方法解一元二次方程》练习题 题型：填空题

    若方程x2-m=0有整数根，则m的值可以是_______________（只填一个）

    1（答案不唯一） 【解析】【解析】 若方程x2-m=0有整数根，则x=±，只要m为正整数，且m是完全平方数即可．故m可以取1．故答案为：1（答案不唯一）．

    查看答案和解析>>

    科目：初中数学 来源：人教版初中数学九年级上册第二十一章《配方法解一元二次方程》练习题 题型：单选题

    下列各命题中正确的是（ ）

    ①方程x2=-4的根为x1=2，x2=-2

    ②∵（x-3）2=2，∴x-3=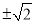，即x=3±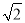

    ③∵x2-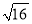=0，∴x=±4

    ④在方程ax2+c=0中，当a＞0，c＞0时，一定无实根

    A. ①② B. ②③ C. ③④ D. ②④

    D 【解析】【解析】 ①x2=-4＜0，任何实数的平方一定是非负数，故①错误， ②正确； ③∵x2-=0，∴ ，∴，∴x=±2．故③错误； ④正确． 故正确的命题是②④．故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学人教版上册：第2章 整式的加减 单元测试卷 题型：单选题

    下面的计算正确的是（　　）

    A. 6a﹣5a=1 B. a+2a2=3a3 C. ﹣（a﹣b）=﹣a+b D. 2（a+b）=2a+b

    C 【解析】试题分析：A．6a﹣5a=a，故此选项错误； B．a与不是同类项，不能合并，故此选项错误； C．﹣（a﹣b）=﹣a+b，故此选项正确； D．2（a+b）=2a+2b，故此选项错误； 故选C．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型：填空题

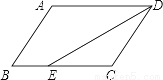
    如图，在?ABCD中，已知AD=8cm，AB=6cm，DE平分∠ADC，交BC边于点E，则BE=________cm．

    2 【解析】∵?ABCD∴∠ADE=∠DEC∵DE平分∠ADC∴∠ADE=∠CDE∴∠DEC=∠CDE∴CD=CE ∵CD=AB=6cm∴CE=6cm∵BC=AD=8cm∴BE=BC-EC=8-6=2cm．

    查看答案和解析>>

    同步练习册答案