
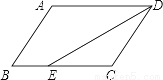
如图,在?ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC,交BC边于点E,则BE=________cm.
 考前必练系列答案
考前必练系列答案科目:初中数学 来源:人教版初中数学九年级上册第二十一章《配方法解一元二次方程》练习题 题型:解答题
若规定两数a、b通过“※”运算,得到4ab,即a※b=4ab,例如2※6=4×2×6=48
(1)求3※5的值;
(2)求x※x+2※x-2※4=0中x的值;
(3)若无论x是什么数,总有a※x=x,求a的值.
(1) x1=2,x2=-4;(2) x1=2,x2=-4;(3) 【解析】试题分析:要注意a※b=4ab新定义的运算方法,把已知数按照运算法则代入即可求值,后两问将数值代入后得到了两个方程,解方程即可. 试题解析:【解析】 (1)∵a※b=4ab,∴3※5=4×3×5=60; (2)由x※x+2※x﹣2※4=0得,4x2+8x﹣32=0,即x2+2x﹣8=0,∴x1=2,x2...查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期末达标检测卷 题型:解答题
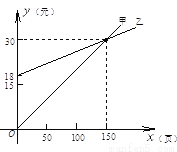
某人因需要经常去复印资料,甲复印社按A4纸每10页2元计费,乙复印社则按A4纸每10页1元计费,但需按月付一定数额的承包费. 两复印社每月收费情况如图所示,根据图中提供的信息解答下列问题:
(1)乙复印社要求客户每月支付的承包费是 元.
(2)当每月复印 页时,两复印社实际收费相同.
(3)如果每月复印页在250页左右时,应选择哪一个复印社?请简单说明理由.
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期末达标检测卷 题型:单选题
如图,正方形ABCD的边长为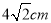 ,则图中阴影部分的面积为( )cm2.
,则图中阴影部分的面积为( )cm2.
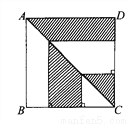
A. 8 B. 6 C. 16 D. 不能确定
C 【解析】根据正方形是轴对称图形,可知阴影部分的面积正好是正方形面积的一半,可知阴影部分的面积为×÷2=16. 故选:C.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:解答题
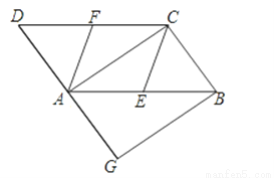
如图,在?ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
(1)求证:CE∥AF;
(2)若∠G=90°,求证:四边形CEAF是菱形.
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:填空题
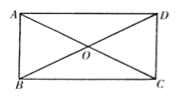
如图,矩形ABCD中,对角线AC=8cm,?AOB是等边三角形,则AD的长为 cm.
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学 第18章 平行四边形 单元检测卷 题型:单选题
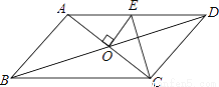
如图,在?ABCD中,AB=3,BC=5,对角线AC、BD相交于点O.过点O作OE⊥AC,交AD于点E.连接CE,则△CDE的周长为( )
A. 3 B. 5 C. 8 D. 11
C 【解析】根据平行四边形的性质, ∴AO=OC, ∵OE⊥AC, ∴OE为AC的垂直平分线, ∴AE=EC, ∴△CDE的周长为:CD+AD=5+3=8, 故选C.查看答案和解析>>
科目:初中数学 来源:福建省莆田市秀屿区2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在平面直角坐标系中,点A是函数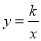
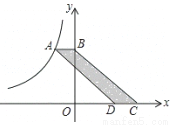
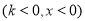 图象上的点,过点A与y轴垂直的直线交y轴于点B,点C、D在x轴上,且BC∥AD.若四边形ABCD的面积为3,则k值为___________.
图象上的点,过点A与y轴垂直的直线交y轴于点B,点C、D在x轴上,且BC∥AD.若四边形ABCD的面积为3,则k值为___________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年河南省南阳市镇平县七年级(上)12月月考数学试 题型:填空题
n为整数,则(﹣1)2n+(﹣1)2n+1=_____.
0 【解析】试题解析: 故答案为:0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com