
下列基本图形中,经过平移、旋转或轴对称变换后,不能得到如图的是( )
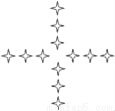
A.  B.
B.  C.
C.  D.
D. 
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期末测评 题型:解答题
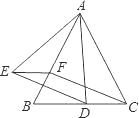
如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级上学期期末考试数学试卷 题型:单选题
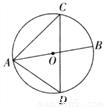
如图,AB是⊙O的直径,CD是⊙O的弦,连接 AC,AD,若∠ADC=55°,则∠CAB的度数为( )
A. 35° B. 45° C. 55° D. 65°
A 【解析】【解析】 连接BC.∵AB是⊙O的直径,∴∠ACB=90°.又∵∠ADC=55°,∴∠B=55°,∴∠BAC=90°﹣55°=35°.故选A.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型:单选题
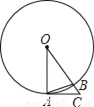
如图,A、B是⊙O上的两点,AC是⊙O的切线,∠OBA=75°,⊙O的半径为1,则OC的长等于( )
A. 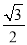 B.
B. 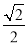 C.
C. 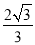 D.
D. 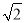
查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号)
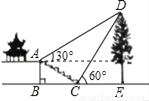
查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:填空题
如图,A,B是反比例函数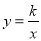 图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为3,则k的值为_____.
图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为3,则k的值为_____.
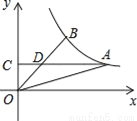
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:解答题
如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于A(1,0)、B(4,0)两点,与y轴交于C(0,2),连接AC、BC.
(1)求抛物线解析式;
(2)BC的垂直平分线交抛物线于D、E两点,求直线DE的解析式;
(3)若点P在抛物线的对称轴上,且∠CPB=∠CAB,求出所有满足条件的P点坐标.
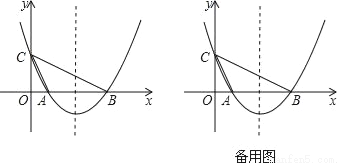
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:单选题
如图在Rt△ABC中,∠A=90°,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:
①AE=CF;
②S四边形AEDF=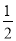 S△ABC;
S△ABC;
③DE≤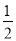 AB;
AB;
④AD与EF可能互相垂直,其中正确结论的个数是
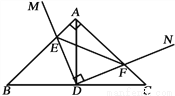
A. 4 B. 3 C. 2 D. 1
B 【解析】 (2)S四边形AEDF= ③ (4)AD与EF可能互相垂直 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com