
一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
D. 【解析】 试题分析:设内角和为1080°的多边形的边数是n,则(n﹣2)•180°=1080°,解得:n=8. 则原多边形的边数为7或8或9.故选D. 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
由五个小立方体搭成如图的几何体,从正面看到的平面图形是( )
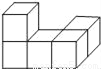
A. 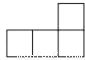 B.
B. 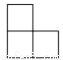 C.
C. 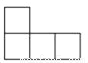 D.
D. 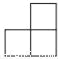
查看答案和解析>>
科目:初中数学 来源:山东省寿光市2017-2018学年七年级上期末模拟数学试卷 题型:填空题
如图所示的图形绕虚线旋转一周得到的几何体的名称是________.
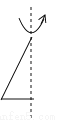
查看答案和解析>>
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(2) 题型:填空题
一个圆弧形门拱的拱高为1米,跨度为4米,那么这个门拱的半径为________米.
2.5. 【解析】设半径为rm,则查看答案和解析>>
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(2) 题型:单选题
如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为( )
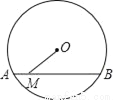
A. 2 B. 3 C. 4 D. 5
B 【解析】试题分析:根据垂线段最短可知,当时,线段OM的值最小 此时,连接OA,由垂径定理可知, 在查看答案和解析>>
科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:解答题
我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.
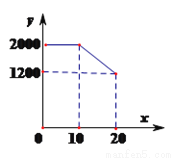
(1)求y与x之间的函数关系式;
(2)老张种植柑橘的成本是800元/吨,当客商采购量是多少时,老张在这次销售柑橘时获利最大?最大利润是多少?
(1)y = ?80x + 2800; (2)当张经理的采购量为12.5吨时,老王在这次买卖中所获得的利润最大,最大利润为12500元. 【解析】(1)当0 < x ≤ 10时,y = 2000. 当10 < x ≤ 20时,设BC满足的函数关系式为y = kx + b,则 . 解得k = ?80,b = 2800,∴y = ?80x + 2800. (2)当0...查看答案和解析>>
科目:初中数学 来源:2017年吉林省中考数学一诊试卷 题型:填空题
如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A﹣C﹣B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C﹣B﹣A向A点运动,当其中一点运动到终点时,两点同时停止运动.设运动时间为t秒,当t=_____秒时,△PCQ的面积等于8cm2.
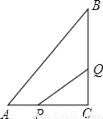
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:解答题
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=3,AB=4,求菱形ADCF的面积.
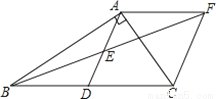
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:单选题
如图,A,B,C为⊙O上三点,若∠ACB=20°,则∠BAO的大小为( )
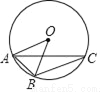
A. 40° B. 60° C. 70° D. 80°
C 【解析】∵∠ACB=20°, ∴∠AOB=2×20°=40°, ∵AO=BO, ∴∠BAO=∠OBA=(180°?40°)÷2=70°, 故选:C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com