
﹣6的绝对值等于( )
A. 6 B.  C. ﹣
C. ﹣ D. ﹣6
D. ﹣6
科目:初中数学 来源:人教版七年级下册数学 第十章 数据的收集 整理与描述 单元检测卷 题型:填空题
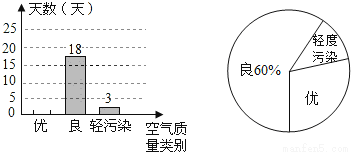
小明从市环境监测网随机查阅了若干天的空气质量数据作为样本进行统计,分别绘制了如图的条形统计图和扇形统计图,根据图中提供的信息,可知扇形统计图中表示空气质量为优的扇形的圆心角的度数为 .
查看答案和解析>>
科目:初中数学 来源:2017-2018学年甘肃省天水市七年级(上)期末数学试卷 题型:解答题
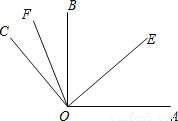
如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠AOC和∠COB的度数.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年甘肃省天水市七年级(上)期末数学试卷 题型:填空题
比较大小:﹣6_____﹣8(填“<”、“=”或“>”)
> 【解析】绝对值大的负数反而小查看答案和解析>>
科目:初中数学 来源:2017-2018学年甘肃省天水市七年级(上)期末数学试卷 题型:单选题
在墙壁上固定一根横放的木条,则至少需要钉子的枚数是( )
A. 1枚 B. 2枚 C. 3枚 D. 任意枚
B 【解析】【解析】 ∵两点确定一条直线, ∴至少需要2枚钉子. 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册 第2章 有理数及其运算 单元测试 题型:解答题
计算:
(1)6.8-(-4.2)+(-9); (2)|-2|-(-3)×(-15);
(3)( 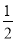 +
+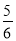 -
-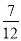 )×(-24); (4)-24÷(
)×(-24); (4)-24÷(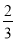 )2+3
)2+3 ×(-
×(- )-(-0.5)2.
)-(-0.5)2.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学北师大版上册 第2章 有理数及其运算 单元测试 题型:填空题
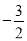 的倒数的绝对值_____.
的倒数的绝对值_____.
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第六章《实数--立方根》同步练习 题型:解答题
已知2a-1的平方根是±3,3a-b+2的算术平方根是4,求a+3b的立方根.
2 【解析】试题分析:根据平方根与算术平方根的定义得到3a-b-2=16,2a-1=9,则可计算出a=5,b=1,然后计算a+b后利用立方根的定义求解. 试题解析∵2a-1的平方根是±3 ∴a=5 ∵3a-b+2的算术平方根是4,a=5 ∴b=1 ∴a+3b =8 ∴a+3b的立方根是2查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2017-2018学年七年级上学期期末质量检测数学试卷 题型:解答题
阅读下列材料:
我们知道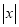 的几何意义是在数轴上数
的几何意义是在数轴上数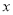 对应的点与原点的距离;即
对应的点与原点的距离;即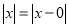 ;这个结论可以推广为
;这个结论可以推广为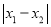 表示在数轴上数
表示在数轴上数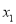 ,
, 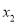 对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
例1:解方程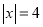 .
.
容易得出,在数轴上与原点距离为4的点对应的数为±4,即该方程的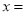 ±4;
±4;
例2:解方程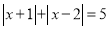 .
.
由绝对值的几何意义可知,该方程表示求在数轴上与-1和2的距离之和为5的点对应的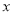 的值.在数轴上,-1和2的距离为3,满足方程的
的值.在数轴上,-1和2的距离为3,满足方程的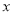 对应的点在2的右边或在-1的左边.若
对应的点在2的右边或在-1的左边.若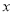 对应的
对应的
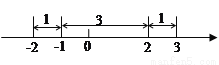
点在2的右边,如图可以看出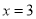 ;同理,若
;同理,若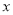 对应点在-1的左边,可得
对应点在-1的左边,可得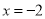 .所以原方程的解是
.所以原方程的解是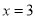 或
或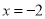 .
.
例3:解不等式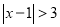 .
.
在数轴上找出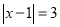 的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的
的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的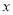 值就满足
值就满足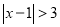 ,所以
,所以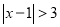 的解为
的解为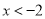 或
或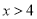 .
.
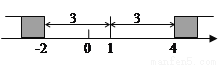
参考阅读材料,解答下列问题:
(1)方程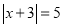 的解为 ;
的解为 ;
(2)方程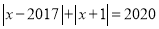 的解为 ;
的解为 ;
(3)若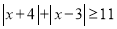 ,求
,求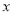 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com