
如图,△ABC中,CD⊥AB,垂足为D.下列条件中,能证明△ABC是直角三角形的有 (多选、错选不得分).
①∠A+∠B=90°
②AB2=AC2+BC2
③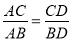
④CD2=AD•BD.
科目:初中数学 来源:2017年湖南省郴州市汝城县濠头学校中考数学模拟试卷 题型:填空题
某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位.要求租用的车辆不留空座,也不能超载.有 种租车方案.
2 【解析】 试题分析:设租8座车x辆,4座车y辆,根据题意可得8x+4y=20,当x=1时,y=3;当x=2时,y=1,因此共有2种组车方案.查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学模拟试卷 题型:解答题
有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3cm、7cm、9cm;乙盒子中装有4张卡片,卡片上分别写着2cm、4cm、6cm、8cm;盒子外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
(1) ;(2) . 【解析】分析:(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与这三条线段能组成三角形的情况,再利用概率公式求解即可求得答案;(2)首先由树状图求得这三条线段能组成直角三角形的情况,然后直接利用概率公式求解即可求得答案. 本题解析: (1)画树状图得: ∵共有12种等可能的结果,这三条线段能组成三角形的有7种情况, ∴这三条线段能组...查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学模拟试卷 题型:单选题
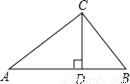
在娱乐节目“墙来了!”中,参赛选手背靠水池,迎面冲来一堵泡沫墙,墙上有人物造型的空洞.选手需要按墙上的造型摆出相同的姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一块几何体恰好能以右图中两个不同形状的“姿势” 分别穿过这两个空洞,则该几何体为( )
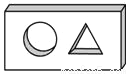
A. 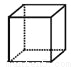 B.
B. 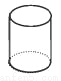 C.
C. 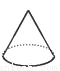 D.
D. 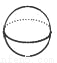
查看答案和解析>>
科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:单选题
如图:将一个矩形纸片ABCD,沿着BE折叠,使C、D点分别落在点C1,D1处.若∠C1BA=50°,则∠ABE的度数为( )
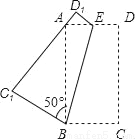
A. 15° B. 20° C. 25° D. 30°
B 【解析】根据折叠前后对应角相等可知. 【解析】 设∠ABE=x, 根据折叠前后角相等可知,∠C1BE=∠CBE=50°+x, 所以50°+x+x=90°, 解得x=20°. 故选B. “点睛”本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.查看答案和解析>>
科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:单选题
下列剪纸图形中,既是轴对称图形又是中心对称图形的有( )

A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】试题解析:根据轴对称图形和中心对称图形的概念可知:第2、4二个图形既是轴对称图形又是中心对称图形. 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省徐州市区联校2017-2018学年七年级上学期期中联考数学试卷 题型:填空题
若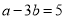 ,则
,则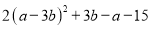 =________.
=________.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:解答题
一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
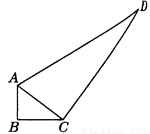
【答案】面积等于36
【解析】试题分析:利用勾股定理求AC,再利用勾股定理逆定理求∠ACB=90°,分别求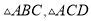 的面积.
的面积.
试题解析:
 ∠B=90°,AB=3,BC=4,AC=
∠B=90°,AB=3,BC=4,AC=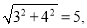
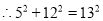 =169,
=169,
所以∠ACD=90°,
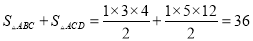 .
.
所以面积是36.
【题型】解答题
【结束】
22
如图,在所给正方形网格(每个小网格的边长是1)图中完成下列各题.
(1)格点△ABC(顶点均在格点上)的面积=_________;
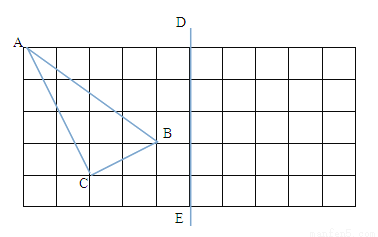
(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点P,使PB+PC最小,并求出这个最小值.
(1)面积等于5(2)图形见解析(3)最小值是根号17 【解析】试题分析:(1)利用勾股定理求出三角形边长,并证明是直角三角形求面积.(2)画出A,B,C的对称点A1,B2,C3,连接三角形.(3)利用对称利用两点之间直线最短求最小值. 试题解析: (1)分别利用勾股定理求得AC=2,AB=,BC=, ,所以∠ACB=90°,面积等于=5. (2)画出A,B,C的对称点A1...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com