
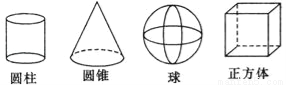
下面四个几何体中,主视图与俯视图不同的共有( )
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】试题分析:主视图是从正面看到的图形,俯视图是从物体的上面看到的图形,可根据各几何体的特点进行判断.圆柱的主视图是矩形,俯视图是圆,它的主视图与俯视图不同;圆锥的主视图是等腰三角形,俯视图是圆,它的主视图与俯视图不同;球体的三视图均为圆,故它的主视图和俯视图相同;正方体的三视图均为正方形,故它的主视图和俯视图也相同;所以主视图与俯视图不同的是圆柱和圆锥,故选B.科目:初中数学 来源:江苏省无锡市2017-2018学年七年级12月月考数学试卷 题型:解答题
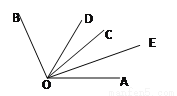
如图,已知∠AOC=40°,∠BOC=80°,OD平分∠AOB.
求(1)∠COD的度数;
(2)若OE是∠AOC的角平分线,求∠EOD的度数.
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
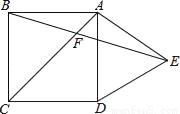
如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( )
A. 75° B. 60° C. 55° D. 45°
B 【解析】分析:本题考查的是正方形的性质和等腰三角形和等边三角形的性质. 解析:因为AC为正方形的对角线,所以∠BAC=∠CAD=45°,因为三角形ADE为等边三角形,所以∠DAE=60°,∴∠BAD=150°,∵AB=AE,∴∠BAE=15°,∴∠BFC=60°. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年陕西师大附中中考数学二模试卷 题型:填空题
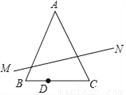
如图,△ABC中,AB=AC,∠BAC=45°,BC=2,D是线段BC上的一个动点,点D是关于直线AB、AC的对称点分别为M、N,则线段MN长的最小值是_____.
查看答案和解析>>
科目:初中数学 来源:2017年陕西师大附中中考数学二模试卷 题型:单选题
如果点A(m,n)、B(m﹣1,n﹣2)均在一次函数y=kx+b(k≠0)的图象上,那么k的值为( )
A. 2 B. 1 C. ﹣1 D. ﹣2
A 【解析】试题解析:∵点A(m,n)、B(m-1,n-2)均在一次函数y=kx+b(k≠0)的图象上, ∴ 解得:k=2. 故选A.查看答案和解析>>
科目:初中数学 来源:广东省深圳市2017-2018北师大版八年级(上)数学期末模拟试卷 题型:解答题
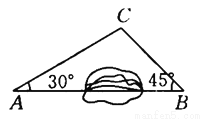
如图所示,A,B两地之间有一座山,汽车原来从A地到B地需要经C地沿折线A—C—B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10 km,∠A=30°,∠B=45°,则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果精确到0.1 km,参考数据: 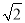 ≈1.41,
≈1.41, 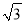 ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源:广东省深圳市2017-2018北师大版八年级(上)数学期末模拟试卷 题型:填空题
若关于x,y的二元一次方程组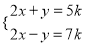 的解满足方程
的解满足方程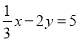 ,则k=_________.
,则k=_________.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省武汉市中考数学模拟试卷 题型:解答题
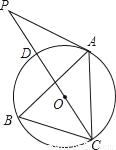
如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
(1)求证:AP是⊙O的切线;
(2)求PD的长.
查看答案和解析>>
科目:初中数学 来源:2017年浙江省台州市中考数学二模试卷 题型:单选题
下列图形中,是中心对称但不是轴对称图形的为( )
A. 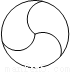 B.
B. 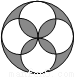 C.
C. 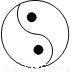 D.
D. 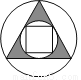
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com