
��ͼ����6��8�������У�ÿ��С�����εı߳���Ϊ1����O�͡�ABC�Ķ����ΪС�����εĶ��㣮
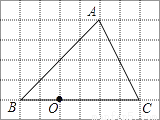
��1����ͼ�С�ABC���ڲ�����A��B��C�䣬ʹ��A��B��C��͡�ABCλ�ƣ���λ������Ϊ��O��λ�Ʊ�Ϊ1��2��
��2�����ӣ�1���е�AA�䣬���߶�AA��ij�����________��
(1)��ͼ����������2��. ����������������� ��1������OA���ֱ�����OA��OB��OC���е�A�䡢B�䡢C�䣬��˳�����������㼴�ɵõ����������Σ� ��2���ɵ�O����A���Ǹ����ͼ�κ��ɶ�������õ�AO�ij��ȣ��ɵ�OA��:OA=1:2�������AA��ij���. ��������� ��1������ͼ����A��B��C��Ϊ������ ��2����ͼ��Ϲ��ɶ����ɵã�AO=�� �ߵ�OA...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�γ���2017-2018ѧ����꼶12���¿���ѧ�Ծ� ���ͣ������
����M��a��3���͵�N��2��a+b������x��Գƣ���b��ֵΪ ��
��5 �������� �������������x��ԳƵ������������ȣ������껥Ϊ�෴��.��������ã�a=2��a+b=��3����ã�a=2��b=��5.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����а�����2016-2017ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
Ҫʹ��ʽ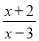 �����壬��x��ȡֵӦ����(���� )
�����壬��x��ȡֵӦ����(���� )
A. x�٣�2 B. x��3 C. x����2 D. x����3
B �����������������������ã�x+3��0�� ���x��-3�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����в�2017-2018ѧ����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ���ѡ��
��ͼ����B=��D=90�㣬CB=CD����1=30�㣬���2=��������
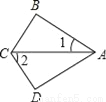
A. 30�� B. 40�� C. 50�� D. 60��
D �������������������Rt��ABC��Rt��ADC�У���BC=DC��AC=AC����Rt��ABC��Rt��ADC��HL�������2=��ACD���ߡ�1+��ACD=90�㣬���2+��1=90�㣬�ߡ�1=40�㣬���2=50�㣬��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����������������2017���п���ѧһģ�Ծ� ���ͣ������
��ͼ��������y=ax2+bx+c��a��0����x�ύ��A����4��0����B��2��0������y�ύ�ڵ�C��0��2����
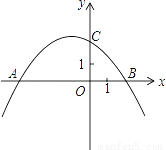
��1���������ߵĽ���ʽ��
��2������DΪ���������ϵ�һ�����㣬����ֱ��AC�Ϸ�������A��C��DΪ�����������������ʱ�����D�����꼰��ʱ�����ε������
��3����ABΪֱ������M��ֱ�߾�����E����1����5�����������M���У����ֱ�ߵĽ���ʽ��
��1��y=��x2��x+2����2��2��D������Ϊ����2��2������3��y=x����y=��x���� ����������������� ��1������֪�������������߽���ʽΪ�� ���ٴ����C�����꣨0��2����õ�ֵ���ɵõ������ߵĽ���ʽ�� ��2����ͼ2������D��DH��AB��H����ֱ��AC�ڵ�G����A��C���������ֱ��AC�Ľ���ʽ�����D�ĺ�����Ϊ��m��������ú���m���Ĵ���ʽ�����DG�ij������S��ADC=D...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����������������2017���п���ѧһģ�Ծ� ���ͣ������
��ͼ����OΪλ�����Ľ��ı���ABCD�Ŵ��õ��ı���A��B��C��D�䣬��OA=4��OA��=8�����ı���ABCD���ı���A��B��C��D����ܳ��ı�Ϊ________��
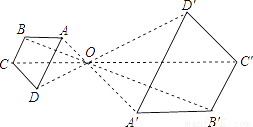
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����������������2017���п���ѧһģ�Ծ� ���ͣ���ѡ��
������������y=  ��ͼ���㣨2��3����������ͼ��Ҳһ�������ĵ��ǣ� ��
��ͼ���㣨2��3����������ͼ��Ҳһ�������ĵ��ǣ� ��
A. ����3����2�� B. ��2����3�� C. ��3����2�� D. ����2��3��
A ��������������������������k=2��3=6�����Է�������������ʽΪy=���ߩ�3������2��=6��2������3��=��6��3������2��=��6����2��3=��6����㣨��3����2���ڷ���������y=��ͼ���ϣ���ѡA���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ������
��֪�㣨��1��y1������2��y2������3��y3���ڷ���������y=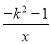 ��ͼ���ϣ����á���������y1��y2��y3Ϊ_____��
��ͼ���ϣ����á���������y1��y2��y3Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ ������÷� ���ͣ������
��ͼ������ѧ����У�С��Ϊ�˲���У�����CD�ĸ߶ȣ����ڽ�ѧ¥�ĵ�A�㴦���۲��˶���C�����ǡ�CAD=60�㣬Ȼ��������ѧ¥�ϵ�B�����۲��˵�D�ĸ�����30�㣬��֪��ѧ¥AB��4�ף�
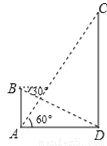
��1�����ѧ¥����˵�ˮƽ����AD��������������ţ�
��2�������CD�ĸ߶ȣ�
��1��4m����2��12m. �������� �����������1����������ó���ADB=30�㣬��������������Ǻ�����ϵ�ó�AD�ij�����2�����ã�1���������CD=AD•tan60������𰸣� �����������1���߽�ѧ¥B�㴦�۲��˵�D�ĸ�����30�㣬 ���ADB=30�㣬 ��Rt��ABD�У���BAD=90�㣬��ADB=30�㣬AB=4m�� ��AD===4��m���� �𣺽�...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com