
在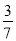 ,0,
,0, 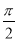 ,-2017,0. 01001这五个数中,无理数有( )
,-2017,0. 01001这五个数中,无理数有( )
A. 1个 B. 2个 C. 3个 D. 4个
A 【解析】无理数是指无限不循环小数,包括三方面的数:①含π的,②一些有规律的数,③开方开不尽的数,所以只有是无理数, 故选A. 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
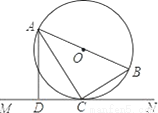
如图,AB是⊙O的直径,C是⊙O上一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.求证:MN是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:填空题
据统计,参加今年扬州市初中毕业、升学统一考试的学生约36800人,这个数据用科学记数法表示为_________。
3.68×104 【解析】 .查看答案和解析>>
科目:初中数学 来源:2017年河南省中考数学三模试卷 题型:填空题
如图,A,B是反比例函数 图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为3,则k的值为_____.
图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为3,则k的值为_____.

查看答案和解析>>
科目:初中数学 来源:2017年河南省中考数学三模试卷 题型:单选题
反比例函数y=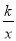 (k≠0)图象上的两个点A(x1,y1),B(x2,y2),当x1<x2<0时,y1>y2,那么一次函数y= -2kx +k的图象不经过( )
(k≠0)图象上的两个点A(x1,y1),B(x2,y2),当x1<x2<0时,y1>y2,那么一次函数y= -2kx +k的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
C 【解析】∵当x1查看答案和解析>>
科目:初中数学 来源:湖北省黄冈市2017-2018学年七年级上学期第三次学力检测数学试卷 题型:单选题
已知|a|=5,b2=16,且ab<0,那么a-b的值为( )
A. ±1 B. ±9 C. 1或9 D. -1或-9
B 【解析】∵, ∴, 又∵, ∴当时, ;当时, ; ∴或, 即. 故选B.查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
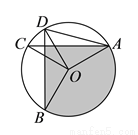
如图,在⊙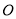 中,弦
中,弦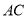 ,
, 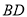 相交于点
相交于点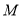 ,且
,且 .
.
( )求证:
)求证: 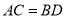 ;
;
( )若
)若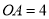 ,
, 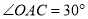 ,当
,当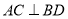 时,求:
时,求:
①图中阴影部分面积.
②弧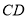 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
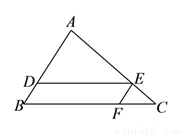
如图,在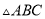 中,点
中,点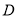 ,
, 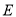 ,
, 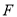 分别在边
分别在边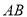 ,
, 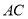 ,
, 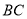 上,且
上,且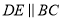 ,
, 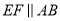 .若
.若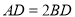 ,则
,则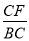 的值为( ).
的值为( ).
A. 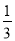 B.
B. 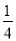 C.
C. 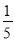 D.
D. 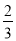
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型:填空题
等腰三角形一腰上的高与另一腰的夹角为40°,则等腰三角形顶角的度数是 ________
50或130 【解析】首先根据题意画出图形, 一种情况等腰三角形为锐角三角形,①如图1, ∵BD⊥AC,∠ABD=40°, ∴∠A=50°, 即顶角的度数为50°. 另一种情况等腰三角形为钝角三角形,②如图2, ∵BD⊥AC,∠DBA=40°, ∴∠BAD=50°, ∴∠BAC=130°. 故答案为:50或130.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com