
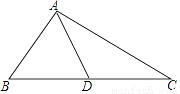
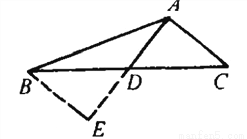
如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=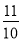 ,则tan∠BAD=________.
,则tan∠BAD=________.
【答案】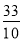
【解析】延长AD到E,使AD=DE,CF 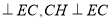 ,
,
在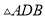 与
与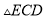 ,
,
,  ,所以
,所以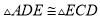 ,
,
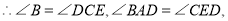
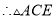 是等腰三角形,s
是等腰三角形,s
设EM= x,DE=11,MC=10,
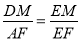 ,
,
 ,
,
 x=
x=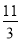 ,
,
 tan∠BAD=
tan∠BAD=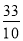 .
.
故答案为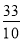 .
.
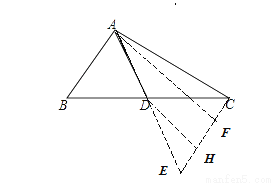
点睛:倍长中线法构造全等三角形,如图,AD是中线,令AD=DE,则 ADC全等
ADC全等 EBD.
EBD.
【题型】填空题
【结束】
21
先化简,再求值: 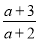 ÷(
÷(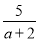 -a+2),其中a=2sin60°+3tan45°.
-a+2),其中a=2sin60°+3tan45°.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:单选题
如图是有一些相同的小正方体构成的立体图形的三视图.这些相同的小正方体的个数是( )

A. 4 B. 5 C. 6 D. 7
B 【解析】根据题意可知: 第一行第一列只能有1个正方体, 第二列有3个正方体, 第一行第3列有1个正方体, 共需正方体1+3+1=5. 故选:B.查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:解答题
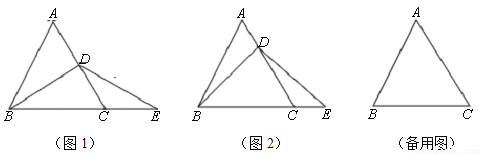
如图,△ABC是等边三角形,点D在AC上,点E在BC的延长线上,且BD=DE.
(1)若点D是AC的中点,如图1,求证:AD=CE
(2)若点D不是AC的中点,如图2,试判断AD与CE的数量关系,并证明你的结论:(提示:过点D作DF∥BC,交AB于点F)
查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:单选题
若a≠b,下列各式中不能成立的是
A. 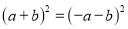 B.
B. 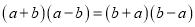
C. 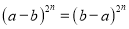 D.
D. 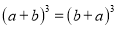
查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:解答题
某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
【答案】(1)A种品牌套装每套进价为10元,B种品牌套装每套进价为7.5元;(2)最少购进A品牌工具套装17套.
【解析】试题分析:(1)利用两种套装的套数作为等量关系列方程求解.(2)利用总获利大于等于120,解不等式.
试题解析:
(1)【解析】
设B种品牌套装每套进价为x元,则A种品牌套装每套进价为(x+2.5)元.
根据题意得: 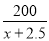 =2×
=2×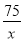 ,
,
解得:x=7.5,
经检验,x=7.5为分式方程的解,
∴x+2.5=10.
答:A种品牌套装每套进价为10元,B种品牌套装每套进价为7.5元.
(2)【解析】
设购进A品牌工具套装a套,则购进B品牌工具套装(2a+4)套,
根据题意得:(13﹣10)a+(9.5﹣7.5)(2a+4)>120,
解得:a>16,
∵a为正整数,
∴a取最小值17.
答:最少购进A品牌工具套装17套.
点睛:分式方程应用题:一设,一般题里有两个有关联的未知量,先设出一个未知量,并找出两个未知量的联系;二列,找等量关系,列方程,这个时候应该注意的是和差分倍关系:三解,正确解分式方程;四验,应用题要双检验;五答,应用题要写答.
【题型】解答题
【结束】
26
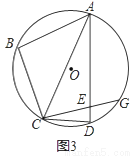
四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.
(1)如图1,求证:CE=CD;
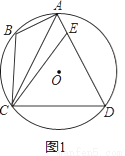
(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;
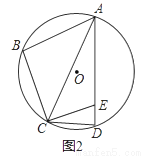
(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC= 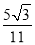 ,EG=2,求AE的长.
,EG=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:填空题
抛物线y=3(x﹣2)2+5的顶点坐标是 .
【答案】(2,5).
【解析】试题分析:由于抛物线y=a(x﹣h)2+k的顶点坐标为(h,k),由此即可求解.
【解析】
∵抛物线y=3(x﹣2)2+5,
∴顶点坐标为:(2,5).
故答案为:(2,5).
考点:二次函数的性质.
【题型】填空题
【结束】
16
在半径为1的圆中,120°的圆心角所对的弧长是 .
. 【解析】 试题分析:此题主要考查了扇形的弧长计算公式,正确的代入数据并进行正确的计算是解题的关键.根据弧长公式:l= 计算即可. 【解析】 ∵圆心角为120°,R=1,∴l===.故答案为.查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:单选题
如图,一边靠学校院墙,其它三边用40米长的篱笆围成一个矩形花圃,设矩形ABCD的边AB=x米,面积为S平方米,则下面关系式正确的是( )

A. S=x(40﹣x) B. S=x(40﹣2x) C. S=x(10﹣x) D. S=10(2x﹣20)
【答案】B
【解析】AB=x米,面积为S平方米,
S=x(40﹣2x).
故选B.
【题型】单选题
【结束】
9
把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )
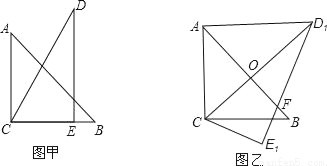
A. 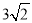 B. 5 C. 4 D.
B. 5 C. 4 D. 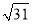
查看答案和解析>>
科目:初中数学 来源:江西省抚州市2017-2018年上学期九年级数学期末试卷 题型:解答题
用适当的方法解下列一元二次方程:
(1)2x2+4x-1=0;(2)(y+2)2-(3y-1)2=0.
(1)x1=-1+,x2=-1-;(2)y1=-,y2=. 【解析】试题分析:(1)根据方程的特点,利用公式法解一元二次方程即可; (2)根据因式分解法,利用平方差公式因式分解,然后再根据乘积为0的方程的解法求解即可. 试题解析:(1)∵a=2,b=4,c=-1 ∴△=b2-4ac=16+8=24>0 ∴x== ∴x1=-1+,x2=-1- (2)(y+2...查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:解答题
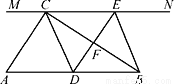
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com