
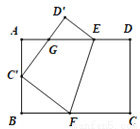
��ͼ��������ABCD��EF�۵���ʹ����Cǡ������AB�ߵ�C'������D���ڵ�D'����C'D'���߶�AE�ڵ�G.
��1����֤����BC'F�ס�AGC'��
��2����C'��AB���е㣬AB=6��BC=9����AG�ij�.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��ɽ��ʡ������������2016-2017��ѧ�ڰ��꼶��ĩ��ѧ�����Ծ� ���ͣ������
��֪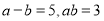 ����
����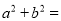 ___________________.
___________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ̩�����п���ѧ��ģ�Ծ� ���ͣ������
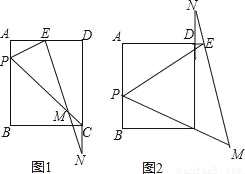
��ͼ1������ABCD�У�P��AB���ϵ�һ�㣨����A��B�غϣ���PEƽ�֡�APC������AD��E����E��EM��PE��ֱ��CP��M����ֱ��CD��N��
��1����֤��CM=CN��
��2����AB��BC=4��3��
�ٵ�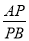 =�� ��ʱ��Eǡ����AD���е㣻
=�� ��ʱ��Eǡ����AD���е㣻
����ͼ2������PEM���PBC����ʱ����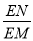 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ̩�����п���ѧ��ģ�Ծ� ���ͣ������
���Ϧ�=32��22�䣬��Ϧ�����ǵĶ���Ϊ_____��
57��38' ���������������� 90�㩁�Ϧ�=90�㩁32��22��=57��38'���ʴ�Ϊ��57��38'���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꽭��ʡ̩�����п���ѧ��ģ�Ծ� ���ͣ���ѡ��
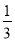 ���෴���ǣ�������
���෴���ǣ�������
A. ��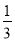 B. 3 C. ��3 D.
B. 3 C. ��3 D. 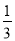
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������������У����2018����꼶��ѧ����ĩѧҵ�����ѧ�Ծ� ���ͣ������
��ͼ����ABC�ڽ��ڡ�O��AD��BC�ڵ�D��AD=BD.����O�İ뾶OB=2����AC�ij�Ϊ____��
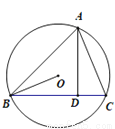
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������������У����2018����꼶��ѧ����ĩѧҵ�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ����һ��ֱ������������ABC����BAC=90�㣬D��AC���е㣬�ִ����г�һ������ֽ��DEFG������E,F��BC�ϣ���G��AB�ϣ���BF=4.5cm��CE=2cm����ֽ��GD�ij�Ϊ�� ��
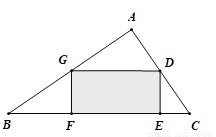
A. 3 cm B. 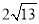 cm C.
cm C. 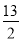 cm D.
cm D. 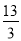 cm
cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�긣��ʡ������ܼ��������ѧУ���꼶���ϣ�������ѧ�Ծ� ���ͣ������
�����˩�5�ף�ʵ������_____��_____�ף�����Ⱥ�ƽ���100������100�ף���ô+3800�ױ�ʾ_____��
�½��� 5�� �Ⱥ�ƽ���3800�� �������������˩�5�ף�ʵ�������½���5�ף� ����Ⱥ�ƽ���100������100�ף���ô+3800�ױ�ʾ�Ⱥ�ƽ���3800�ף� �ʴ�Ϊ����1���½�����2��5����3���Ⱥ�ƽ���3800�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����ɹų�������꼶���ϣ�������ѧ�Ծ� ���ͣ������
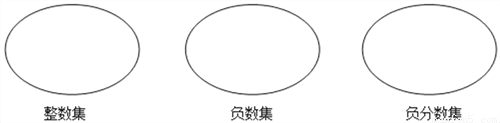
�����и��������ʾ�����ڵ�������Ȧ�
��18�� 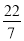 ��3.1416��0��2001����
��3.1416��0��2001����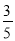 ����0.142857��95%��
����0.142857��95%��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com