
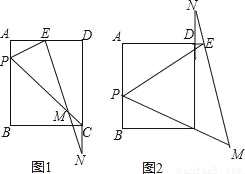
如图1,矩形ABCD中,P是AB边上的一点(不与A,B重合),PE平分∠APC交射线AD于E,过E作EM⊥PE交直线CP于M,交直线CD于N.
(1)求证:CM=CN;
(2)若AB:BC=4:3,
①当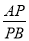 = 时,E恰好是AD的中点;
= 时,E恰好是AD的中点;
②如图2,当△PEM与△PBC相似时,求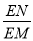 的值.
的值.
科目:初中数学 来源:江苏省2016-2017学年七年级上学期期末考试数学试卷 题型:解答题
由几个相同的边长为1的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个几何体的正视图和左视图.
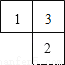
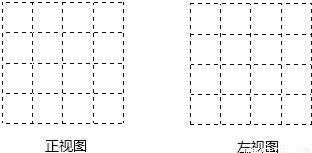
(2)根据三视图,请你求出这个组合几何体的表面积(包括底面积).
(1)详见解析;(2)24. 【解析】试题分析:(1)主视图有2列,每列小正方形数目分别为1,3;左视图有2列,每列小正方形数目分别为3,2;由此画出这个几何体的正视图和左视图即可;(2)上下共有2×3个正方形;左右共有5×2个正方形;前后共有4×2个正方形.由此即可得这个组合几何体的表面积为(3+4+5)×2=24. 试题解析: (1)图形如下所示 (2)几何体的表面积为...查看答案和解析>>
科目:初中数学 来源:山东省临沂市沂南县2016-2017上学期八年级期末数学调研试卷 题型:单选题
下列计算中,正确的是( )
A. 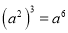 B.
B. 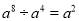 C.
C. 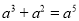 D.
D. 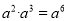
查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版七年级数学下册 期中测评 题型:填空题
游客爬山所用时间t(单位:h)与山高h(单位:km)间的函数关系如图所示,请写出游客爬山的过程: __________________.
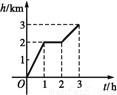
查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版七年级数学下册 期中测评 题型:单选题
下列计算正确的是( )
A. -3x2y·5x2y=2x2y B. -2x2y3·2x3y=-2x5y4
C. 35x3y2÷5x2y=7xy D. (-2x-y)(2x+y)=4x2-y2
C 【解析】试题分析:A、-3x2y·5x2y=-15x4y2,故此选项错误; B、-2x2y3·2x3y=-4x5y4,故此选项错误; C、35x3y2÷5x2y=7xy,故此选项正确; D、 (-2x-y)(2x+y)=-4x2-y2+4xy,故此选项错误. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年江苏省泰州市中考数学三模试卷 题型:解答题
学校准备添置一批课桌椅,原计划订购60套,每套100元.店方表示:如果多购可以优惠.结果校方购了72套,每套减价3元,但商店获得同样多的利润.求每套课桌椅的成本.
每套课桌椅成本82元. 【解析】【解析】 设每套课座椅的成本为元. 则 解得 经检验, 符合题意. 答:每套课座椅的成本为82元.查看答案和解析>>
科目:初中数学 来源:2017年江苏省泰州市中考数学三模试卷 题型:填空题
圆锥的母线长为6cm,底面圆半径为4cm,则这个圆锥的侧面积为_____ cm2.
24π 【解析】试题解析:∵圆锥的底面半径为4cm, ∴圆锥的底面圆的周长=2π•4=8π, ∴圆锥的侧面积=×8π×6=24π(cm2).查看答案和解析>>
科目:初中数学 来源:浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型:解答题
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C'处,点D落在点D'处,C'D'交线段AE于点G.
(1)求证:△BC'F∽△AGC';
(2)若C'是AB的中点,AB=6,BC=9,求AG的长.
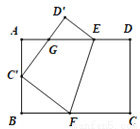
查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古通辽市八年级(下)期末数学试卷 题型:解答题
已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
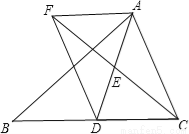
(1)求证:AF=DC;
(2)若AD=CF,试判断四边形AFDC是什么样的四边形?并证明你的结论.
见解析;矩形. 【解析】试题分析:因为AF∥DC,E为AD的中点,即可根据AAS证明△AEF≌△DEC,故有AF=DC;由(1)知,AF=DC且AF∥DC,可得四边形AFDC是平行四边形,又因为AD=CF,故可根据对角线相等的平行四边形是矩形进行判定. 试题解析:(1)∵AF∥DC, ∴∠AFE=∠DCE, 又∵∠AEF=∠DEC(对顶角相等),AE=DE(E为AD的中点), ∴...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com