练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

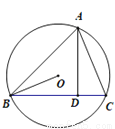
    如图，△ABC内接于⊙O，AD⊥BC于点D，AD=BD.若⊙O的半径OB=2，则AC的长为____．

    【解析】延长AO交⊙O与点E，连接BE,则AE=2OB=4. ∵AD⊥BC，AD=BD, ∴ . ∵∠E=∠C, ∠ABE=∠ADC=90°, ∴△ABE∽△ADC, ∴ , ∴, ∴ , ∴AC=.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省临沂市沂南县2016-2017上学期八年级期末数学调研试卷 题型：单选题

    如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为（　　）

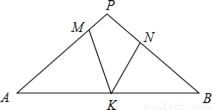
    A. 44° B. 66° C. 88° D. 92°

    D 【解析】分析：本题考察等腰三角形的性质，全等三角形的判定，三角形的外角定理. 解析：∵PA=PB，∴∠A=∠B，∵AM=BK，BN=AK， ∴ 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省泰州市中考数学三模试卷 题型：解答题

    学校准备添置一批课桌椅，原计划订购60套，每套100元．店方表示：如果多购可以优惠．结果校方购了72套，每套减价3元，但商店获得同样多的利润．求每套课桌椅的成本．

    每套课桌椅成本82元． 【解析】【解析】 设每套课座椅的成本为元． 则 解得 经检验， 符合题意． 答：每套课座椅的成本为82元．

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省泰州市中考数学三模试卷 题型：单选题

    一个几何体的表面展开图如图所示，则这个几何体是(　　)

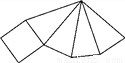
    A. 四棱锥 B. 四棱柱 C. 三棱锥 D. 三棱柱

    A 【解析】试题分析：根据四棱锥的侧面展开图得出答案. 试题解析：如图所示：这个几何体是四棱锥. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型：解答题

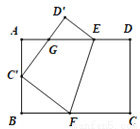
    如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的C'处，点D落在点D'处，C'D'交线段AE于点G.

    （1）求证：△BC'F∽△AGC'；

    （2）若C'是AB的中点，AB=6，BC=9，求AG的长.

    （1）证明见解析；（2）. 【解析】试题分析：（1）由余角的性质可得∠BF C'=∠A C'G，然后根据两个角对应相等的两个三角形相似判断； （2）先由勾股定理求出BF的长，然后利用相似三角形的性质列比例式求解. （1）证明：由题意可知∠A=∠B=∠GC'F=90°， ∴∠BF C'+∠B C'F= 90°，∠A C'G+∠B C'F= 90°, ∴∠BF C'=∠A...

    查看答案和解析>>

    科目：初中数学 来源：浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型：单选题

    如图，点A,B,C均在坐标轴上，AO=BO=CO=1，过A,O,C作⊙D，E是⊙D上任意一点，连结CE, BE，则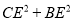的最大值是（ ）

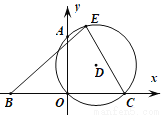
    A. 4 B. 5 C. 6 D.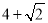

    C 【解析】∵∠AOC=90°, ∴AC是直径. ∵点A. B.C均在坐标轴上，OB=OC=OA=1， ∴A(0,1),B(-1,0),C(1,0)； ∴ ，AC=， 设点E的坐标为(m,n)， ∵点E在D上， ∴(m?)2+(n?)2=， ∴m2+n2=m+n①， ∵B(-1,0),C(1,0)， ∴CE2+BE2=(m-1)2...

    查看答案和解析>>

    科目：初中数学 来源：浙江省温州市瑞安市五校联考2018届九年级上学期期末学业检测数学试卷 题型：单选题

    二次函数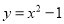的图象与y轴的交点坐标是（ ）

    A. （0，1） B. （1，0） C. （－1，0） D. （0，－1）

    D 【解析】当x=0时， y=0-1=-1, ∴图象与y轴的交点坐标是（0,-1）. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年福建省漳州市芗城区玉兰学校七年级（上）期中数学试卷 题型：单选题

    当1＜a＜2时，代数式|a﹣2|+|1﹣a|的值是（ ）

    A. ﹣1 B. 1 C. 3 D. ﹣3

    B 【解析】知识点是代数式求值及绝对值，根据a的取值范围，先去绝对值符号，再计算求值． 【解析】 当1＜a＜2时， |a﹣2|+|1﹣a|=2﹣a+a﹣1=1． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年内蒙古赤峰市七年级（上）期中数学试卷 题型：填空题

    观察下列算式：21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，…通过观察，用所发现的规律确定22017的个位数字是___________________.

    2 【解析】【解析】 ∵2017÷4=504…1，∴22017的个位数字是2，故答案为：2．

    查看答案和解析>>

    同步练习册答案