
函数y=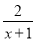 的图象可能是( )
的图象可能是( )
A. 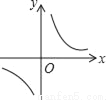 B.
B. 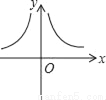 C.
C. 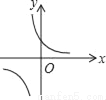 D.
D. 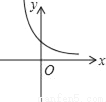
科目:初中数学 来源:广西南宁市2017年中考数学一模试卷 题型:单选题
小张抛掷两枚质地均匀的硬币,出现两枚硬币全部正面朝上的概率是( )
A. 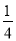 B.
B. 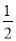 C.
C. 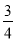 D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市江夏区2017-2018学年八年级(上)期中数学试卷 题型:解答题
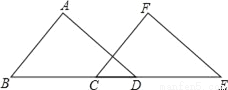
如图,在△ABD和△FEC中,点B、C、D、E在同一直线上,且AB=FE,BC=DE,∠B=∠E,求证:∠ADB=∠FCE.
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学三模试卷 题型:解答题
如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.
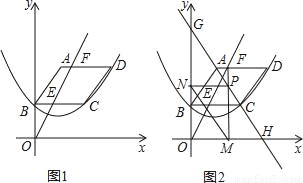
(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
(1)抛物线解析式为y=x2﹣x+3;(2)S=m﹣3(2<m≤6);(3)当m=时,MN最小=. 【解析】试题分析:(1)根据平行四边形的性质和抛物线的特点确定出点D,然而用待定系数法确定出抛物线的解析式.(2)根据AD∥BC∥x轴,且AD,BC间的距离为3,BC,x轴的距离也为3,F(m,6),确定出E(,3),从而求出梯形的面积.(3)先求出直线AC解析式,然后根据FM⊥x轴,表示出点...查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学三模试卷 题型:填空题
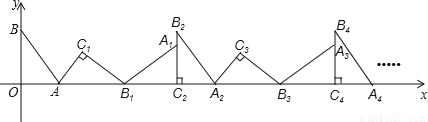
如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(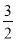 ,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
,0),B(0,2),则B2的坐标为_____;点B2016的坐标为_____.
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学三模试卷 题型:单选题
分式方程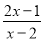 =1的解为( )
=1的解为( )
A. x=﹣1 B. x=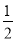 C. x=1 D. x=2
C. x=1 D. x=2
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学三模试卷 题型:单选题
下列各数:1.414,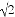 ,-
,- ,0,其中是无理数的是( )
,0,其中是无理数的是( )
A. 1.414 B. 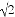 C. -
C. - D. 0
D. 0
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017-2018学年七年级上期中试卷数学试卷 题型:填空题
我国载人飞船按一定的轨道绕着地球飞行,一圈的路程约为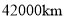 .用科学记数法表示
.用科学记数法表示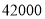 为__________.
为__________.
查看答案和解析>>
科目:初中数学 来源:福建省2017-2018学年七年级上学期期中考试数学试卷 题型:解答题
先化简,再求值。
2(ab-5ab2)-(2ab2-ab),其中a=﹣1,b=2
42 【解析】试题分析:本题考查了整式的化简求值,整式的化简就是去括号合并同类项,化简后再把a=﹣1,b=2代入求值. 【解析】 原式=2ab-10a-2a+ab =3ab-12a 当 a=﹣1,b=2时, 原式=3ab-12a=3×(-1)×2-12×(-1)× =-6+48 =42查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com