练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

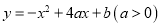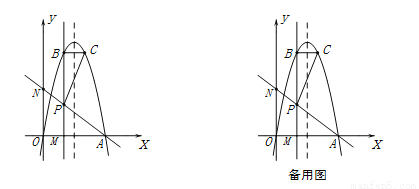
    抛物线与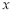轴相交于O、A两点（其中O为坐标原点），过点P（2，2a）作直线PM⊥x轴于点M，交抛物线于点B，点B关于抛物线对称轴的对称点为C（其中B、C不重合），连接AP交y轴于点N，连接BC和PC．

    （1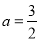）时，求抛物线的解析式和BC的长；

    （2）如图时，若AP⊥PC，求的值；

    （3）是否存在实数，使，若存在，求出的值；若不存在，请说明理由．

    （1），BC=2；（2）；（3）. 【解析】 试题分析：（1）由抛物线与轴相交于O、A两点（其中O为坐标原点），得到b=0，故抛物线为，把代入，得到P（2，3）和，由对称轴x=2，即可得到BC的长； （2）把x=2代入，得到B（2，），设C（x， ），由对称轴，得到C（， ），由，得到A（4a，0），由AP⊥PC，得到，即，解方程即可得到结论； （3）由OA=4a， OM=...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型：填空题

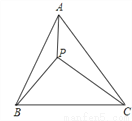
    如图，点P是等边△ABC内一点，PA=6，PB=8，PC=10，则△APC的面积是__________

    【解析】把△APC绕点A顺时针旋转60°，使点P旋转到点D，连接PD；作BE⊥AP交AP的延长线与点E. 由旋转的性质得， AD=AP=6,BD=PC=10，∠DAP=60°, ∴△ADP是等边三角形， ∴∠APD=60°,DP=AP=6. ∵62+82=102， ∴DP2+BP2=BD2， ∴△BPD是直角三角形， ∴∠BPD=90°, ∴∠...

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    在—2，—3，0，1四个数中，最小的数是（ ）

    A. —3 B. —2 C. 0 D. 1

    A 【解析】根据正数,负数的性质可得,最小的数是－3,故选A.

    查看答案和解析>>

    科目：初中数学 来源：安徽省2017～2018学年上学期九年级数学期末试卷 题型：单选题

    若（2，5）、（4，5）是抛物线y=ax2+bx+c上的两个点，则它的对称轴是（ ）

    A. x=﹣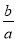 B. x=1 C. x=2 D. x=3

    D 【解析】试题解析：因为点(2,5)、(4,5)在抛物线上， 根据抛物线上纵坐标相等的两点，其横坐标的平均数就是对称轴， 所以,对称轴 故选D.

    查看答案和解析>>

    科目：初中数学 来源：安徽省2017-2018学年九年级上学期期末试卷数学 题型：解答题

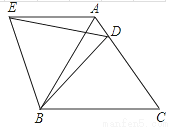
    如图，在等边△ABC中，D是边AC上一点，连接BD．将△BCD绕点B逆时针旋转60°得到△BAE，连接ED．若BC=10，BD=9，求△AED的周长．

    19 【解析】试题分析：先由△ABC是等边三角形得出AC＝AB＝BC＝10，根据图形旋转的性质得出AE＝CD，BD＝BE，故可得出AE＋AD＝AD＋CD＝AC＝10，由∠EBD＝60°，BE＝BD即可判断出△BDE是等边三角形，故DE＝BD＝9，故△AED的周长＝AE＋AD＋DE＝AC＋BD＝19． 试题解析： 【解析】 ∵△ABC是等边三角形， ∴AC＝AB＝BC＝10...

    查看答案和解析>>

    科目：初中数学 来源：安徽省2017-2018学年九年级上学期期末试卷数学 题型：填空题

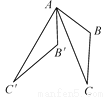
    如图，在△ABC中，∠BAC＝33°，将△ABC绕点A按顺时针方向旋转50°，对应得到△AB′C′，则∠B′AC的度数为____．

    17° 【解析】∵∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′， ∴∠B′AC′=33°,∠BAB′=50°， ∴∠B′AC的度数=50°?33°=17°. 故答案为：17°.

    查看答案和解析>>

    科目：初中数学 来源：安徽省2017-2018学年九年级上学期期末试卷数学 题型：单选题

    用配方法解方程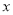2－4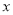＋2＝0，下列配方正确的是（ ）

    A. (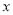－2)2 ＝2 B. (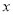＋2)2 ＝2 C. (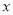－2)2 ＝－2 D. (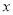－2)2 ＝6

    A 【解析】把方程x2-4x+2=0的常数项移到等号的右边，得到x2-4x=-2， 方程两边同时加上一次项系数一半的平方，得到x2-4x+4=-2+4， 配方得（x-2)2=2， 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：山东省泰安市宁阳县2017-2018学年九年级上学期期末质量检测数学试卷 题型：填空题

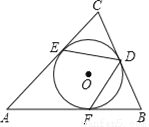
    如图，已知⊙O内切于△ABC，切点分别为D、E、F，若∠A=50°，则∠EDF=__．

    65° 【解析】连接OE、OF， ∵⊙O内切于△ABC，∴∠OEA=∠OFA=90°，∴∠EOF=180°﹣∠A=130°， 由圆周角定理得，∠EDF=∠EOF=65°.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    在直角坐标系中画出一次函数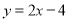的图像，并完成下列问题：

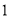    （）此函数图像与坐标轴围成的三角形的面积是______；

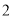    （）观察图像，当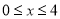时，y的取值范围是______；

    （）将直线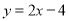平移后经过点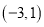，求平移后的直线的函数表达式．

    　　

    （1）4；（ ）；（ ）． 【解析】试题分析：利用“两点确定一条直线”作出函数y=2x-4的图象； （1）分别求出函数图象与x轴、y轴的交点坐标，再利用三角形的面积公式进行求解即可； （2）根据图象可知x=0时，y=-4，x=4时，y=4即可得； （3）设平移后的函数表达式为y=2x+b，将代入，解得b=7，即可得. 试题解析：（1）令y=0，解得x=2， ∴直...

    查看答案和解析>>

    同步练习册答案