
如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为____.
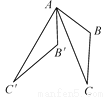
科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:填空题
如图,△ABC绕点A顺时针旋转80°得到△AEF,若∠B=100°,∠F=50°,则∠α的度数是________.
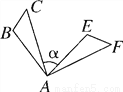
查看答案和解析>>
科目:初中数学 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:解答题
如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.
求证:EF与圆O相切.
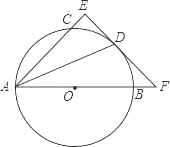
查看答案和解析>>
科目:初中数学 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:单选题
二次函数y=(x﹣1)2﹣2的顶点坐标是( )
A. (﹣1,﹣2) B. (﹣1,2) C. (1,﹣2) D. (1,2)
C 【解析】试题分析:已知解析式为抛物线的顶点式,根据顶点式的坐标特点,直接写出顶点坐标. 【解析】 因为y=(x﹣1)2﹣2是抛物线的顶点式, 根据顶点式的坐标特点,顶点坐标为(1,﹣2). 故选C.查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:解答题
抛物线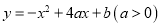 与
与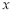 轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
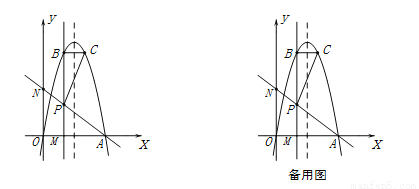
(1)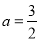 时,求抛物线的解析式和BC的长;
时,求抛物线的解析式和BC的长;
(2)如图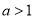 时,若AP⊥PC,求
时,若AP⊥PC,求 的值;
的值;
(3)是否存在实数 ,使
,使 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:单选题
二次函数y= 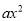 +bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:
+bx+c(a≠0)图象上部分点的坐标(x,y)对应值列表如下:

则该函数图象的对称轴是( ).
A. 直线x=﹣3 B. 直线x=﹣2
C. 直线x=﹣1 D. 直线x=0
B 【解析】根据二次函数图像的对称性,可知其对称轴为x=-2. 故选:B.查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:单选题
下列平面图形中,既是轴对称图形,又是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 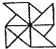
查看答案和解析>>
科目:初中数学 来源:山东省泰安市宁阳县2017-2018学年九年级上学期期末质量检测数学试卷 题型:单选题
如图所示,抛物线y=ax2+bx+c的顶点为B(–1,3),与x轴的交点A在点(–3,0)和(–2,0)之间,以下结论:①b2–4ac=0;②a+b+c>0;③2a–b=0;④c–a=3.其中正确的有( )
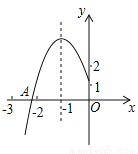
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】试题分析:根据图像可得:二次函数与x轴有两个交点,则,故①错误;根据函数的对称性可知:当x=1时,y0,即a+b+c0,故②错误;根据题意可知:函数的对称轴为直线x=-1,即,则2a-b=0,则③正确;当x=-1时,y=3,则a-b+c=3,根据③可知b=2a,则a-b+c=a-2a+c=c-a=3,故④正确;故本题选B.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
若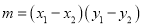 ,且A
,且A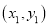 、B
、B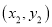 是一次函数
是一次函数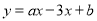 图像上两个不同的点,当
图像上两个不同的点,当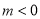 时,a的取值范围是______.
时,a的取值范围是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com