
已知二次函数y=kx2-6x-9的图象与x轴有两个交点,则k的取值范围为( )
A. k>-1 B. k>-1且k≠0 C. k≥-1 D. k<-1且k≠0
B 【解析】由题意得,△>0,且k≠0,即(-6)2-4×k×(-9)>0,且k≠0,所以k>-1且k≠0, 故选B. 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源:湖南邵阳市区2017-2018学年七年级上册数学期末试卷 题型:单选题
如图所示,边长为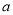 的正方形中阴影部分的面积为( )
的正方形中阴影部分的面积为( )
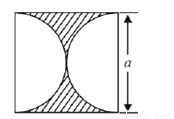
A. 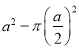 B.
B. 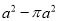 C.
C. 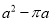 D.
D. 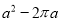
查看答案和解析>>
科目:初中数学 来源:宁夏中卫市2018届九年级(上)期中数学试卷 题型:填空题
菱形的面积为24,其中的一条对角线长为6,则此菱形的周长为_____.
20 【解析】试题解析:如图所示: ∵四边形ABCD是菱形, ∵菱形的面积为24, 即 解得: 在中,由勾股定理得: ∴菱形的周长=4×5=20; 故答案为:20.查看答案和解析>>
科目:初中数学 来源:湖北省十堰市丹江口市2018届九年级(上)期中数学试卷 题型:解答题
如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
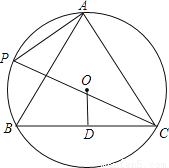
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
(1)证明见解析(2)4 【解析】【解析】 (1)证明:∵∠APC和∠ABC是同弧所对的圆周角,∴∠APC=∠ABC。 又∵在△ABC中,∠BAC=∠APC=60°,∴∠ABC=60°。 ∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°。 ∴△ABC是等边三角形。 (2)连接OB, ∵△ABC为等边三角形,⊙O为其外接圆, ∴O...查看答案和解析>>
科目:初中数学 来源:湖北省十堰市丹江口市2018届九年级(上)期中数学试卷 题型:填空题
若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移1个单位,再沿铅直方向向上平移3个单位,则原抛物线图象的解析式应变为__.
y=x2-1 【解析】将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,这个相当于把抛物线向左平移1个单位,再向下平移3个单位, ∵y=(x-1)2+2, ∴原抛物线图象的解析式应变为y=(x-1+1)2+2-3=x2-1, 故答案为:y=x2-1.查看答案和解析>>
科目:初中数学 来源:湖北省十堰市丹江口市2018届九年级(上)期中数学试卷 题型:单选题
如图,点A,B,C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
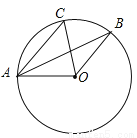
A. 25° B. 50° C. 60° D. 80°
B 【解析】试题分析:先根据OA=OB,∠BAO=25°得出∠B=25°,再由平行线的性质得出∠B=∠CAB=25°,根据圆周角定理即可得出结论. ∵OA=OB,∠BAO=25°,∴∠B=25°. ∵AC∥OB,∴∠B=∠CAB=25°,∴∠BOC=2∠CAB=50°.故选B.查看答案和解析>>
科目:初中数学 来源:浙江省杭州市白马湖2017-2018学年八年级上学期期中数学试卷(含解析) 题型:解答题
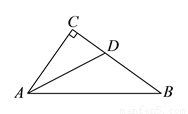
如图, 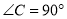 ,
, 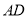 平分
平分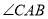 ,
, 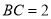 ,
, 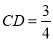 ,求
,求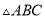 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市白马湖2017-2018学年八年级上学期期中数学试卷(含解析) 题型:单选题
已知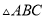 中,
中, 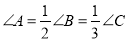 ,则它的三条边之比为( ).
,则它的三条边之比为( ).
A. 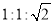 B.
B. 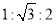 C.
C. 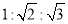 D.
D. 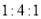
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:填空题
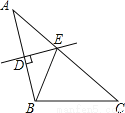
如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com