
ͼ�ٱ�ʾ����ij�ۺ��̳�����1��5�µ���Ʒ���������ܶ�������ͼ�ڱ�ʾ�����̳���װ���������۶�ռ�̳����������ܶ�İٷֱ�������۲�ͼ�١�ͼ�ڣ�����������⣺
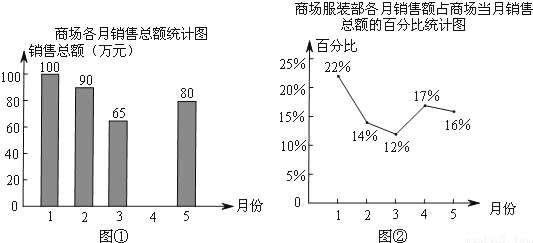
��1�������̳��������ݱ���������̳�1��5�µ���Ʒ�����ܶ�һ����410��Ԫ�����������һ��Ϣ��ͼ���е�ͳ��ͼ����������
��2���̳���װ��5�·ݵ����۶��Ƕ�����Ԫ��
��3��С�չ۲�ͼ�ں���Ϊ��5�·��̳���װ�������۶��4�·ݼ����ˣ���ͬ�����Ŀ�������˵�����ɣ�
��1��75����2��12.8��Ԫ����3��С�յ�˵���Ǵ���� �������������������1�������ܶ��ȥ��֪���µ����۶���ɵõ�4�·ݵ����۶ ��2���̳���װ��5�·ݵ����۶�=5�·ݵ������ܶ����װ��5�·����۶�ռ���������ܶ�İٷֱȣ� ��3���ֱ������װ��4�·ݺ�5�·ݵ����۶�Ƚϴ�С���ɵó����ۣ� ����������������� ��1��410����100+90+65+80��=410��3... һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�꺣��ʡ�������п���ѧģ���Ծ� ���ͣ������
ij���б�ҵ���ÿһ��ͬѧ�����Լ�����Ƭ��ȫ������ͬѧ����һ����Ϊ���ȫ�����2550����Ƭ�����ȫ����x��ѧ�����������⣬���з��� ��
x��x��1��=2550�� ��������������������ȫ����x��ѧ������ôÿ��ѧ������Ƭx��1�ţ�ȫ��Ӧ������Ƭx��x��1������ô����������еķ��̣� �������� ȫ����x��ѧ������ôÿ��ѧ������Ƭx��1�ţ� ȫ��Ӧ������Ƭx��x��1���� ����з���Ϊ��x��x��1��=2550�� �ʴ�Ϊx��x��1��=2550���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꺣��ʡ�п���ѧģ���Ծ� ���ͣ������
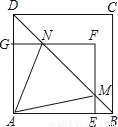
��ͼ������AEFG�Ķ���E��G�ֱ���������ABCD��AB��AD���ϣ�����B����EF�ڵ�M����FG�ڵ�N����AE=a��AG=b��AB=c��b��a��c����
��1����֤�� 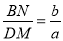 ��
��
��2�����AMN���������a��b��c�Ĵ���ʽ��ʾ����
��3������MAN=45��ʱ����֤��c2=2ab��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꺣��ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
���������뷨�õ�������4.005���������������˵����������ȷ���ǣ�������
A. ����ȷ����λ B. ����ȷ��0.001
C. ����ȷ�����λ D. ����ȷ��ʮλ
D �����������������������4.005��ȷ��ʮλ�� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ����ˣ� ���ͣ������
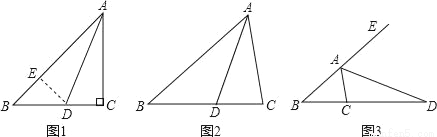
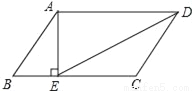
�ڡ�ABC�У���ACB=2��B����ͼ�٣�����C=90�㣬ADΪ��BAC�Ľ�ƽ����ʱ����AB�Ͻ�ȡAE=AC������DE����֤AB=AC+CD��
��1����ͼ�ڣ�����C��90�㣬ADΪ��BAC�Ľ�ƽ����ʱ���߶�AB��AC��CD����������������ϵ������Ҫ֤������ֱ��д����IJ��룺
��2����ͼ�ۣ���ADΪ��ABC�����ƽ����ʱ���߶�AB��AC��CD����������������ϵ����д����IJ��룬������IJ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ����ˣ� ���ͣ������
ij�����������У�10�˵ijɼ�ͳ�����������10�˳ɼ���ƽ����Ϊ ��
���� | 5 | 4 | 3 | 2 | 1 |
���� | 3 | 1 | 1 | 3 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ����ˣ� ���ͣ���ѡ��
��֪��O1���O2���У�����O1�İ뾶Ϊ1����Բ��Բ�ľ�Ϊ5�����O2�İ뾶Ϊ�� ��
A. 4 B. 6 C. 3��6 D. 4��6
D ���������������ɡ�O1���O2���У�����O1�İ뾶Ϊ1����Բ��Բ�ľ�Ϊ5�����ɷֱ�ӡ�O1���O2���л�����ȥ������Ȼ�������Բλ�ù�ϵ��Բ�ľ�d����Բ�뾶R��r��������ϵ�����ϵ������ô𰸣� ��𣺡������� �ߡ�O1���O2���У���O1�İ뾶Ϊ1����Բ��Բ�ľ�Ϊ5�� ����O1���O2���У����O2�İ뾶Ϊ��5-1=4�� ����O1���O2���У����O2�İ뾶Ϊ��5+...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ɽ��ʡ�������п���ѧ��ģ�Ծ���һ�� ���ͣ������
��ͼ����?ABCD�У�AE��BC������ΪE��AB=5��BC=8��sinB=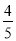 ����ôS��CDE=_____��
����ôS��CDE=_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ����BAC=130�㣬��MP��QN�ֱ�ֱƽ��AB��AC�����PAQ����( )
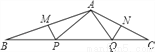
A. 50�� B. 75�� C. 80�� D. 105��
C ����������������������������ڽǺͶ����ɵã���B+��C=180��-130��=50�㣬�����д��ߵ����ʿɵã���BAP=��B����CAQ=��C�����BAP+��CAQ=��B+��C=50�㣬���PAQ=��BAC-(��BAP+��CAQ)=130��-50��=80�㣬��ѡC���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com