练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    方程x2=x的根是__________．

    x1=0，x2=1 【解析】x2-x=0 x(x-1)=0, 所以x1=0，x2=1.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型：解答题

    观察下列各式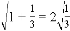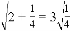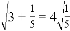：， ， …请你将发现的规律用含自然数n（n≥1）的代数式表达来_____________。

    【答案】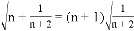

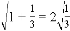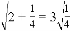    【解析】由①，② ③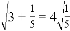，可得从1开始，一个数n加上n+2的倒数再开方等于n+1乘以n+2的倒数再开方，即；

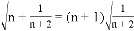    故答案是：。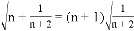

    点睛：规律是：从1开始，一个数n加上n+2的倒数再开方等于n+1乘以n+2的倒数再开方。

    【题型】填空题
    【结束】
    15

    计算：

    （1）

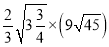
    （2）．

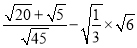    (1)45;(2)1- 【解析】试题分析：（1）利用二次根式的乘法法则运算 （2）先把各二次根式化简为最简二次根式，然后进行二次根式的除法和乘法运算． 试题解析： （1）原式 == 45； （2）原式 =﹣ = 1﹣．

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：解答题

    解方程：(x-1)2-2(x2-1)=0.(因式分解法)

    x1=1，x2=﹣3． 【解析】(x-1)2-2(x2-1)=0. (x-1)2 -2(x-1)(x+1)=0, (x-1)[x-1-2(x+1)]=0, (x-1)(-x-3)=0, x-1=0,-x-3=0, x1=1，x2=-3.

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：解答题

    解方程：x2﹣5x﹣36=0.(因式分解法)

    x1=9，x2=﹣4. 【解析】(x﹣9)(x+4)=0， x-9=0,x+4=0, 所以x1=9，x2=﹣4.

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：填空题

    方程x2﹣4=0的解是___________.

    x=2或-2 【解析】x2﹣4=0, (x-2)(x+2)=0, 所以x1=2，x2=-2.

    查看答案和解析>>

    科目：初中数学 来源：天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习（含答案） 题型：填空题

    方程x(x-1)=x的解是_________．

    x1=0，x2=2 【解析】x(x-1)-x=0， x (x-1-1)=0, x (x-2)=0, 所以x1=0，x2=2.

    查看答案和解析>>

    科目：初中数学 来源：江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型：解答题

    如图，点A的坐标为（4，0）．点P是直线y= x+3在第一象限内的点，过P作PMx轴于点M，O是原点．

    （1）设点P的坐标为（x，y），试用它的纵坐标y表示△OPA的面积S；

    （2）S与y是怎样的函数关系？它的自变量y的取值范围是什么？

    （3）如果用P的坐标表示△OPA的面积S，S与x是怎样的函数关系？它的自变量的取值范围是什么？

    （4）在直线y= x+3上求一点Q，使△QOA是以OA为底的等腰三角形．

    （1）S=2y；（2））S是y的正比例函数，自变量y的取值范围是0＜y＜3；（3）S=x+6，S是x的一次函数，自变量的取值范围是0＜x＜6；（4）Q的坐标为（2，2）． 【解析】试题分析：（1）先求OA长，再找P点的纵坐标，计算面积. （2）利用函数定义知，是正比例函数,范围根据图象可知. （3）由（1）可知，可得到S是x的函数关系. （4）△QOA是以OA为底的等腰三角...

    查看答案和解析>>

    科目：初中数学 来源：江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型：填空题

    如图，已知BC=EC，∠BCE=∠ACD，添加一个条件，使△ABC≌△DEC，你添加的条件是__________（答案不唯一，只需填一个）

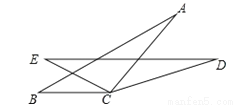
    AC=CD（答案不唯一）． 【解析】添加条件：AC=CD， ∵∠BCE=∠ACD， ∴∠ACB=∠DCE， 在△ABC和△DEC中， ， ∴△ABC≌△DEC（SAS）， 故答案为：AC=CD（答案不唯一）．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年上学期苏州市初三数学期末综合检测 题型：解答题

    如图，在中，，是的中点，以为直径的⊙交的边于点、、.

    (1)求证:四边形是平行四边形;

    (2)若，求的度数.

    （1）见解析；（2）40° 【解析】试题分析：（1）连接DF，由直角三角形斜边上的中线性质得出BD=CD=AD，由圆周角定理可知DF⊥BC，证出DE∥BC，证明DE是△ABC的中位线，由三角形中位线定理得出DE=BC=BF，即可得出结论； （2）连接OG，由等腰三角形的性质得出∠DCA═∠A=35°，由三角形的外角性质得出∠ODG=∠A+∠DCA=70°，由等腰三角形的性质和三角形内角...

    查看答案和解析>>

    同步练习册答案