
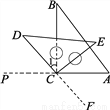
如图是小明自制对顶角的“小仪器”示意图:
(1)将直角三角板ABC的AC边延长且使AC固定;
(2)另一个三角板CDE的直角顶点C与前一个三角板的直角顶点C重合;
(3)延长DC,∠PCD与∠ACF就是一组对顶角,已知∠1=30°,求∠ACF.
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源:北师大版数学七年级下册第一章1.3同底数幂的除法课时练习 题型:单选题
a2m+2÷a等于( )
A. a3m B. 2a2m+2 C. a2m+1 D. am+a2m
C 【解析】试题解析:a2m+2÷a=a2m+1,故C项正确. 故选C.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册 第1章 整式的乘除 章节检测题 题型:填空题
已知a+b=4,a-b=3,则a2-b2= .
12。 【解析】试题分析:a2-b2=(a+b)(a-b)=4×3=12.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.1.1 相交线与平行线 同步练习 题型:单选题
已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )
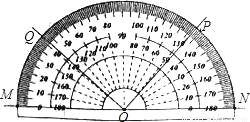
A. ∠NOQ=42° B. ∠NOP=132° C. ∠PON比∠MOQ大 D. ∠MOQ与∠MOP互补
C 【解析】试题分析:如图所示:∠NOQ=138°,选项A错误;∠NOP=48°,选项B错误;如图可得∠PON=48°,∠MOQ=42°,所以∠PON比∠MOQ大,选项C正确;由以上可得,∠MOQ与∠MOP不互补,选项D错误.故答案选C.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下2.1.1 相交线与平行线 同步练习 题型:单选题
如图,∠1和∠2是对顶角的是( )\
A. 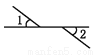 B.
B. 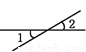 C.
C. 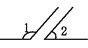 D.
D. 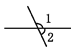
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步练习题 含答案 题型:单选题
如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP的长不可能是( )
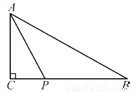
A. 2.5 B. 3 C. 4 D. 5
A 【解析】在△ABC中,∠C=90°,AC=3,根据垂线段最短,可知AP的长不可小于3,当P和C重合时,AP=3,故选A.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型:解答题
如图,AOB为一条在O处拐弯的河,要修一条从村庄P通向这条河的道路,现在有两种设计方案:一是沿PM修路,二是沿PO修路,如果不考虑其他因素,这两种方案哪个更经济些?它是不是最佳方案?如果不是,请你帮助设计出最佳方案,并简要说明理由.
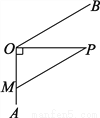
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下1.4.3 多项式与多项式相乘 同步练习 题型:解答题
在一次测试中,甲、乙两同学计算同一道整式乘法:(2x+a)(3x+b),由于甲抄错了第一个多项式中的符号,得到的结果为6x2+11x-10;由于乙漏抄了第二个多项式中的系数,得到的结果为2x2-9x+10.
(1)试求出式子中a,b的值;
(2)请你计算出这道整式乘法的正确结果.
(1)a=-5,b=-2.;(2)6x2-19x+10. 【解析】试题分析:(1)先按甲、乙错误的说法得出的系数的数值求出a,b的值; (2)把a,b的值代入原式求出整式乘法的正确结果. 试题解析:【解析】 (1)由题意得: (2x-a)(3x+b)=6x2+(2b-3a)x-ab,(2x+a)(x+b)=2x2+(a+2b)x+ab, 所以2b-3a=11①, a...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下1.4.2 单项式与多项式相乘 同步练习 题型:解答题
某公园计划砌一个形状如图①所示的喷水池,有人建议改为图②的形状,且外圆的直径不变,只是担心原来备好的材料不够.请你比较两种方案哪一种需要的材料多.
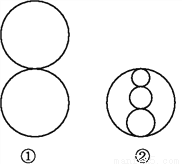
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com