练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

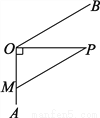
    如图，AOB为一条在O处拐弯的河，要修一条从村庄P通向这条河的道路，现在有两种设计方案：一是沿PM修路，二是沿PO修路，如果不考虑其他因素，这两种方案哪个更经济些？它是不是最佳方案？如果不是，请你帮助设计出最佳方案，并简要说明理由．

    沿PN修最短 【解析】试题分析：根据点到直线的距离定义垂线段最短，进而分析得出即可． 试题解析：∵在Rt△POM中，PM＞PO， ∴这两种方案沿PO修路更经济些， 它不是最佳方案，过点P作PN⊥OB于点N， ∵OP＞PN，PN是点P到OB上的最短路线， ∴此方案是最佳方案．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省长沙市2017-2018学年九年级（上）第一次月考数学试卷 题型：解答题

    为调查广西北部湾四市市民上班时最常用的交通工具的情况，随机抽取了四市部分市民进行调查，要求被调查者从“A：自行车，B：电动车，C：公交车，D：家庭汽车，E：其他”五个选项中选择最常用的一项，将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图，请结合统计图回答下列问题：

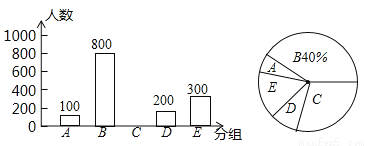
    （1）在这次调查中，一共调查了 名市民，扇形统计图中，C组对应的扇形圆心角是 °；

    （2）请补全条形统计图；

    （3）若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种，则甲、乙两人恰好选择同一种交通工具上班的概率是多少？请用画树状图或列表法求解．

    （1）2000，108；（2）作图见解析；（3）． 【解析】 试题分析：（1）根据B组的人数以及百分比，即可得到被调查的人数，进而得出C组的人数，再根据扇形圆心角的度数=部分占总体的百分比×360°进行计算即可； （2）根据C组的人数，补全条形统计图； （3）根据甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种画树状图或列表，即可运用概率公式得到甲、乙两人恰好选择...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.1.1 相交线与平行线 同步练习 题型：解答题

    如图,A,O,B在同一条直线上,∠AOD=∠BOD=∠EOC=90°,∠BOC∶∠AOE=3∶1.

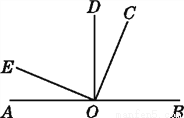
    (1)求∠COD的度数.

    (2)图中有哪几对角互为余角?

    (3)图中有哪几对角互为补角?

    答案见解析. 【解析】试题分析：（1）先求出∠BOC+∠AOE，再根据比值求出∠BOC，然后列式计算即可得解； （2）根据互余的两个角的和等于90°找出即可； （3）根据互补的两个角的和等于180°找出即可． 试题解析:(1)由A,O,B在同一条直线上得∠AOB=180°. 因为∠EOC=90°,所以∠AOE+∠BOC=180°-90°=90°. 又因为∠BOC...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步练习题 含答案 题型：解答题

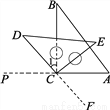
    如图是小明自制对顶角的“小仪器”示意图：

    (1)将直角三角板ABC的AC边延长且使AC固定；

    (2)另一个三角板CDE的直角顶点C与前一个三角板的直角顶点C重合；

    (3)延长DC，∠PCD与∠ACF就是一组对顶角，已知∠1＝30°，求∠ACF.

    60°. 【解析】试题分析：两直线相交，对顶角相等，即∠PCD=∠ACF，然后根据三角板的特点和已知条件来确定∠ACF 试题解析：∵∠PCD=90°?∠1， 又∵∠1=30°， ∴∠PCD=90°?30°=60°， 而∠PCD=∠ACF， ∴∠ACF=60°.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步练习题 含答案 题型：单选题

    已知∠α是锐角，∠α与∠β互补，∠α与∠γ互余，则∠β－∠γ的值等于( )

    A. 45° B. 60° C. 90° D. 180°

    C 【解析】试题分析：根据互余两角之和为90°，互补两角之和为180°，结合题意即可得出答案． 【解析】 由题意得，∠α+∠β=180°，∠α+∠γ=90°， 两式相减可得：∠β﹣∠γ=90°． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型：单选题

    如图，AC⊥BC，点C为垂足，则下列说法错误的是( )

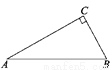
    A. 在线段AB、BC、CA中，AB最长 B. BC的长是点C到直线AB的距离

    C. AC的长是点A到直线BC的距离 D. BC的长是点B到直线AC的距离

    B 【解析】试题解析:A、在直角△ABC中，斜边AB最长，故此说法正确； B、BC的长度是点B到AC的距离，故此说法错误； C、AC的长度是点A到BC的距离，故此说法正确； D、BC的长度是点B到AC的距离，故此说法正确； 故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型：单选题

    如图，已知AB⊥CD于O，直线EF经过点O，与AB的夹角∠AOE＝52°，则∠COF的度数是( )

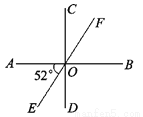
    A. 52° B. 128° C. 38° D. 48°

    C 【解析】试题分析：首先根据垂直定义可得∠AOD=90°，再根据余角定义可计算出∠EOD的度数，再根据对顶角相等可得答案． 【解析】 ∵AB⊥CD， ∴∠AOD=90°， ∵∠AOE=52°， ∴∠EOD=90°﹣52°=38°， ∴∠COF=∠EOD=38°， 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.3 多项式与多项式相乘 同步练习 题型：单选题

    若(x+a)(x-2)的积中不含x项,那么a的值为(　　)

    A. 2 B. -2 C. 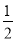D. -

    A 【解析】【解析】 （x+a）（x-2）=x2-2x+ax-2a=x2+（-2+a）x-2a． ∵（x+a）（x-2）的积中不含x项，∴-2+a=0，解得：a=2．故选A．

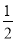
    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.2 单项式与多项式相乘 同步练习 题型：单选题

    今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:-3xy(4y-2x-1)=-12xy2+6x2y+□,□的地方被钢笔水弄污了,你认为□内应填写(　　)

    A. 3xy B. -3xy C. -1 D. 1

    A 【解析】∵左边=-3xy（4y-2x-1）=-12xy2+6x2y+3xy右边=-12xy2+6x2y+□，∴□内上应填写3xy．

    查看答案和解析>>

    同步练习册答案