
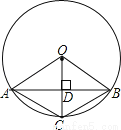
��ͼ����֪�ڡ�O�У�AB���ң��뾶OC��AB������Ϊ��D��Ҫʹ�ı���OACBΪ���Σ�����Ҫ����һ��������������������� ��
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2018�괺�˽̰����꼶��ѧ�²ᣨ��������ĩ���� ���ͣ���ѡ��
��ͼ������С��ӵ�P��0��3������������ʾ�����˶���ÿ��С������������OABC�ı�ʱ����������ʱ����ǵ�������ǣ���С���1�����������εı�ʱ�ĵ�ΪP1����2�����������εı�ʱ�ĵ�ΪP2��������n�����������εı�ʱ�ĵ�ΪPn�����P2 018�������ǣ� ��
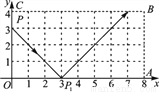
A. ��7��4�� B. ��3��0��
C. ��1��4�� D. ��8��3��
A �������� ��ͼ������6�η�����ص������㣨0��3����������6�� ����P��3���������εı�ʱ����P������Ϊ����8��3���� ��2018=6336+2�� �൱��P��2018���������εı�ʱΪ��337��ѭ����ĵ�2�η����� ��P2 018������Ϊ��7��4���� �ʴ�Ϊ��7��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��ʦ�����ѧ�Ծ���B���� ���ͣ������
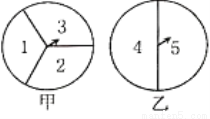
��ͼ����ת�̱��ֳ�3�������ȵ����Ρ���ת�̱��ֳ�2�������ȵ����Σ�С�ĺ�С��������������������ʤ������Ϸ���涨С��ת����һ�Ρ�С��ת����һ��Ϊһ����Ϸ����ָ��ָ�ڱ߽�����ʱ��Ϊ��Ч����ת����
��1��С��˵�����������ָ����ָ�����ڵ���֮��Ϊ6��7�����һ�ʤ���������ʤ������С����ƵĹ�������д�����˻�ʤ�Ŀ����Էֱ��Ƕ���?
��2�������С�ĺ�С�����������Ϸ���һ�ֹ�ƽ����Ϸ������һ�ֺ��ʵķ���(���磺��״ͼ���б�)˵���乫ƽ�ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶��ʦ�����ѧ�Ծ���B���� ���ͣ���ѡ��
��Ʊÿ����ǡ�������������10%����������ԭ�۵�10%�㲻�����ǣ�������ͣ��������ԭ�۵�10%�㲻���ٵ���������ͣ����֪һ֧��Ʊij����ͣ��֮������ʱ�����ǻص�ԭ�ۣ���������˹�Ʊ�ɼ۵�ƽ��������Ϊx����x����ķ����ǣ� ��
A. 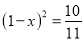 B.
B. 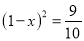 C.
C. 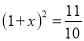 D.
D. 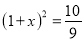
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶����ĩģ����ѧ�Ծ��������棩 ���ͣ������
��ͼ���ó�Ϊ6m�����Ͻ����Ƴɡ��ա����δ���������Ŀ�Ϊxm�������������Ϊym2�����Ͻ����Ŀ��Ȳ��ƣ���
��1�����y��x�ĺ�����ϵʽ��
��2����ΰ��Ŵ���ij��Ϳ�������ʹ�ô������������������ʱ����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶����ĩģ����ѧ�Ծ��������棩 ���ͣ������
��������������Ϊ2cm���ױ߳�Ϊ 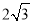 cm����Ϊ________�����Ϊ________��
cm����Ϊ________�����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶����ĩģ����ѧ�Ծ��������棩 ���ͣ���ѡ��
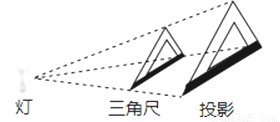
��ͼ�����dz�����ƹ������µ�����ͶӰ�����λ��ͼ�Σ����ǵ����Ʊ�Ϊ2��3�������dzߵ�һ�߳�Ϊ8cm������������ͶӰ�еĶ�Ӧ�߳�Ϊ��������
A. 8cm B. 12cm C. 16cm D. 24cm
B ������������������������Ʊ�Ϊ2��3���ɵó����Ӧ�ߵı�ֵΪ2��3������������ɣ� �������� �����dz�����ƹ������µ�����ͶӰ�����λ��ͼ�Σ����ǵ����Ʊ�Ϊ2��3�����dzߵ�һ�߳�Ϊ8cm�� ������������ͶӰ�еĶ�Ӧ�߳�Ϊ��x����=����ã�x=12�� ��ѡ��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��Ȫ��2017-2018ѧ���һѧ�����꼶��ѧ�Ծ� ���ͣ������
��Ȫ������շѱ�Ϊ����Ϊ5Ԫ��3ǧ��ÿǧ��2.5Ԫ��������1ǧ�װ�1ǧ�Ʒѣ���ij�˳��������ʻ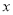 ǧ��(
ǧ��(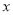 >3)������10Ԫ�����з���Ϊ__________________��
>3)������10Ԫ�����з���Ϊ__________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��ׯ��������2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
���ⱳ�����ڡ�ABC�У�AB��BC��AC���ߵij��ֱ�Ϊ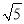 ��
��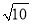 ��
��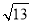 ������������ε����С��ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ1��ʾ�������������ABC�ĸߣ�������������ܼ�������������
������������ε����С��ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ1��ʾ�������������ABC�ĸߣ�������������ܼ�������������
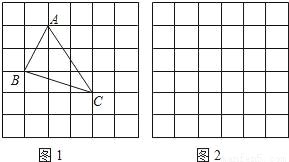
��1�����������������������ABC�������
��2����ͼ2�л���DEF��DE��EF��DF���ߵij��ֱ�Ϊ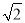 ��
��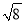 ��
��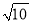
���ж������ε���״��˵�����ɣ�
������������ε��������ֱ��д���𰸣�
��1������2����ͼ���������١�DEF��ֱ�������Σ����ɼ���������2 �������������������1��������Ŀ���õ����ⱳ�������ͼ�ν��м��㼴�ɣ� ��2�����ݹ��ɶ������ҵ�DE��EF��DF�ij��ֱ�Ϊ�������ɹ��ɶ������涨�����жϡ�DEF��ֱ�������Σ� �������� ��1��S��ABC=3��3����1��2����2��3����1��3=�� ��2����ͼ��ʾ�� ��DE=��EF=2��DF=�� ...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com