
���мס��������յ���װ�ӷֱ�ΪA��B������˾��װ�յ����װ�װ��ΪA��˾��װ66̨�յ����Ұ�װ��ΪB��˾��װ60̨�յ����ס������Ӱ�װ�յ����õ���ʱ����ͬ����֪�ӱ��Ҷ�ƽ��ÿ��లװ2̨�յ�����ס���������װ��ƽ��ÿ�����װ�յ���̨����
�װ�װ��ƽ��ÿ�찲װ�յ�22̨���Ұ�װ��ƽ��ÿ�찲װ�յ�20̨. ��������������������еĵ�����ϵ�ǣ��װ�װ��ΪA��˾��װ66̨�յ���ʱ��=�Ұ�װ��ΪB��˾��װ60̨�յ���ʱ�䣻��ƽ��ÿ�찲װ��̨��=�Ҷ�ƽ��ÿ�찲װ��̨��+2����δ֪���������̣���⼴�ɡ� �������� ��װ�װ��ƽ��ÿ�찲װ�յ�x̨��������ã� = �� ��ã�x=22�� �����飺x=22��ԭ��ʽ����... ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ��������У2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
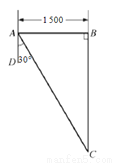
��6�֣���ͼ�������1 500�Ķ�����������̨A��B��ͬʱ�������ֵн�C������̨A����õн�C��������ƫ��30��ķ�������̨B����õн�C���������Ϸ�������н�������̨�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ�������а��꼶��ѧ��ĩ��ϰ�ۺϼ��� ���ͣ���ѡ��
���������������ж�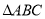 Ϊֱ�������ε��ǣ�������
Ϊֱ�������ε��ǣ�������
A. 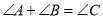 B.
B. 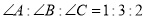
C. 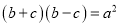 D.
D. 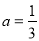 ��
�� 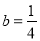 ��
�� 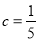
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ӱ�ʡ�ػʵ���¬����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
������������ȷ���ǣ� ��
��ȫ�������ζ�Ӧ����ȣ��������Ƕ�Ӧ��ȵ�����������ȫ�ȣ������߶�Ӧ��ȵ���������ȫ�ȣ��������߶�Ӧ��ȵ���������ȫ�ȡ�
A. 4�� B. 3�� C. 2�� D. 1��
C ����������������ȫ�ȵ����ʿ�֪����ȷ�� �ڸ���ȫ�������ε��ж�������֪AAA������Ϊ�ж����������Ǵ��� �����߶�Ӧ��ȵ��������Σ�����SSS��ȫ�ȣ�������ȷ�� �������߶�Ӧ��ȵ��������Σ��������������ж���������ȫ�ȣ����Ǵ��� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����п�����2017���п���ѧһģ�Ծ� ���ͣ������
���壺���������У���һ�ߵ��е㵽�����ߵĸ��ߵľ�����������ߵ��д��࣮
������ͼ�٣��ڡ�ABC�У�DΪ��BC���е㣬AE��BC��E�����߶�DE�ij�������BC���д��࣮
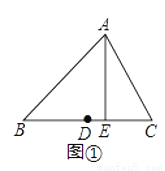
��1����������һ�ߵ��д���Ϊd��d��0������d=0����������������һ����________���ƶϵ���ѧ������________��
��2����ͼ�ڣ��ڡ�ABC�У���B=45�㣬AB=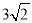 ��BC=8��ADΪ��BC�����ߣ����BC���д��࣮
��BC=8��ADΪ��BC�����ߣ����BC���д��࣮
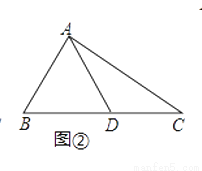
��3����ͼ�ۣ��ھ���ABCD�У�AB=6��AD=4����EΪ��CD���е㣬����AE���ӳ���BC���ӳ����ڵ�F������AC�����ACF�б�AF���д��࣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����п�����2017���п���ѧһģ�Ծ� ���ͣ������
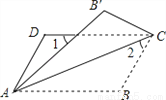
��ͼ����?ABCD�ضԽ���AC�۵���ʹ��B����B�䴦������1=��2=44�㣬���B=_______
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����п�����2017���п���ѧһģ�Ծ� ���ͣ���ѡ��
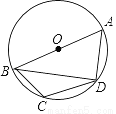
��ͼ���ı���ABCD�ǡ�O���ڽ��ı��Σ�ABΪ��O��ֱ��������BD������BCD=120�㣬���ABD�Ĵ�СΪ�� ��
A. 60��
B. 50��
C. 40��
D. 30��
D �����������ı���ABCD�ǡ�O���ڽ��ı��Σ� ���BAD+��BCD=180�㣬 �ߡ�BCD=120�㣬 ���BAD=60�㣬 ��ABΪ��O��ֱ���� ���ADB=90�㣬 ���ABD=90�㩁60��=30�㣬 �ʴ�Ϊ��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�������żҸ���2016-2017ѧ���һѧ�ڳ�һ��ѧ��ĩ���в��Ծ������𰸣� ���ͣ������
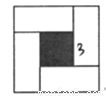
��ͼ���ĸ�һ���ij����κ�һ��С��������ƴ����һ�����������.���������εı߳���7��С�����εı߳���3�����εĶ̱߳�Ϊ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ɽ��ʡ�������п���ѧģ���Ծ� ���ͣ������
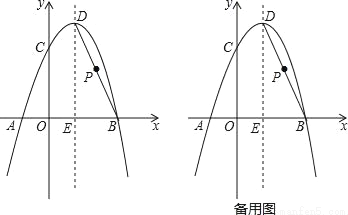
��ͼ��������y=��x2+bx+c����A����1��0����B��3��0�����㣬����y�ύ�ڵ�C����D�������ߵĶ��㣬�����ߵĶԳ���DE��x���ڵ�E������BD��
��1����A��B��C����������ߵĺ�������ʽ��
��2����P���߶�BD��һ�㣬��PE=PCʱ�����P�����ꣻ
��3���ڣ�2���������£�����P��PF��x���ڵ�F��GΪ��������һ���㣬MΪx����һ���㣬NΪֱ��PF��һ���㣬����F��M��N��GΪ������ı�����������ʱ���������M�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com