
菱形的边长是10cm,且菱形的一个内角是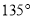 ,则这个菱形的面积的为__________cm2.
,则这个菱形的面积的为__________cm2.
科目:初中数学 来源:北师大版八年级下册数学 第二章 一元一次不等式与一元一次不等式组 单元检测卷 题型:填空题
若(m﹣2)x2m+1﹣1>5是关于x的一元一次不等式,则该不等式的解集为 ________
x<﹣3 【解析】根据不等式是一元一次不等式可得:2m+1=1且m?2≠0,∴m=0, ∴原不等式化为:?2x?1>5,解得x查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第八章《消元解二元一次方程组》同步练习 题型:填空题
《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”译文大致是:“用一根绳子去量一根木条,绳子剩余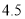 尺;将绳子对折再量木条,木条剩余
尺;将绳子对折再量木条,木条剩余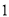 尺,问木条长多少尺?”如果设木条长
尺,问木条长多少尺?”如果设木条长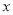 尺,绳子长
尺,绳子长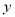 尺,可列方程组为___________;
尺,可列方程组为___________;
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:解答题
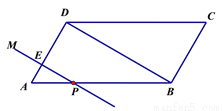
如图,在□ABCD中,AD=4cm,∠A=60°,BD⊥AD.一动点P从A出发,以每秒1cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD.
(1)当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2)当点P运动2秒时,另一动点Q也从A出发沿A→B的路线运动,且在AB上以每秒1cm的速度匀速运动,(当P、Q中的某一点到达终点,则两点都停止运动.)过Q作直线QN,使QN∥PM,设点Q运动的时间为t秒(0≤t≤8),直线PM与QN截□ABCD所得图形的面积为S(cm2).求S关于t的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:填空题
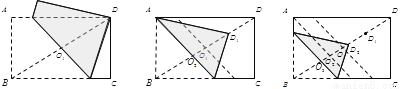
如图,矩形纸片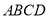 中,
中, 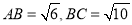 .第一次将纸片折叠,使点
.第一次将纸片折叠,使点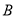 与点
与点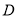 重合,折痕与
重合,折痕与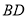 交于点
交于点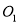 ;设
;设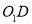 的中点为
的中点为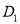 ,第二次将纸片折叠使点
,第二次将纸片折叠使点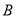 与点
与点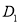 重合,折痕与
重合,折痕与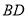 交于点
交于点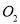 ;设
;设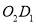 的中点为
的中点为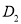 ,第三次将纸片折叠使点
,第三次将纸片折叠使点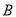 与点
与点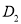 重合,折痕与
重合,折痕与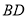 交于点
交于点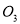 ,… .按上述方法折叠,第n次折叠后的折痕与
,… .按上述方法折叠,第n次折叠后的折痕与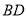 交于点
交于点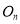 ,则
,则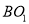 =________,
=________, 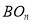 =_________.
=_________.

查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:单选题
小明想知道学校旗杆的高度,他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,则旗杆的高是( ).
A. 8米 B. 10米 C. 12米 D. 14米
C 【解析】 画出示意图如下所示: 设旗杆的高AB为xm,则绳子AC的长为(x+1)m, 在Rt△ABC中,AB2+BC2=AC2, ∴x2+52=(x+1)2, 解得:x=12, ∴AB=12m, 即旗杆的高是12m. 故选D.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:期中达标检测卷 题型:单选题
式子 在实数范围内有意义,则x的取值范围是( ).
在实数范围内有意义,则x的取值范围是( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:北师大版八年级上册数学全册综合测试卷 题型:单选题
下列四个点中,在正比例函数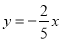 的图象上的点是( )
的图象上的点是( )
A.(2,5)
B.(5,2)
C.(2,-5)
D.(5,-2)
D 【解析】要判断点是否在正比例函数的图象上,只需把点的横坐标代入函数解析式检验纵坐标,若两者相同,则该点在这一正比例函数的图象上,否则不在.因此把选项中各点的坐标分别代入验证,只有(5,-2)适合.查看答案和解析>>
科目:初中数学 来源:湖南省长沙市2017-2018学年九年级(上)第一次月考数学试卷 题型:填空题
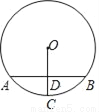
如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8cm,DC=2cm,则OC=_____cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com