练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

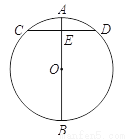
    在我国古代数学著作《九章算术》中记载了这样一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用现代语言表述为：如图，AB为⊙O的直径，弦CD⊥AB于点E，AE = 1寸，CD = 10寸，求直径AB的长．请你解答这个问题.

    直径AB的长26寸． 【解析】试题分析：连接OC．先根据垂径定理求出CE=CD，设半径为r，则OE =r-1，在Rt中， 根据勾股定理求得r的长，即可求解． 试题解析：连接OC， ∵AB为⊙O的直径，弦CD⊥AB于点E，且CD=10， ∴∠BEC＝90°，， 设OC=r，则OA=r，∴OE= ， 在Rt中， ∵， ∴，∴， ∴AB = 2...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京市通州区2017-2018学年第一学期期末初三数学统一检测试卷 题型：填空题

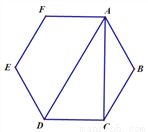
    如图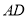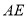， ， 是正六边形的两条对角线.在不添加任何其他线段的情况下，请写出两个关于图中角度的正确结论：（1）__________________________；（2）______________________.

    ∠F=∠E ∠F=120° 【解析】试题解析：【解析】 (1)∠F=∠E；(2)∠F=120°．答案不唯一．故答案为：(1)∠F=∠E；(2)∠F=120°（答案不唯一）．

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    已知： ， ， ．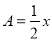

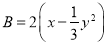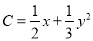    （1）试求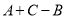所得的结果；（用含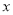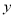， 的式子表示）

    （2）若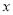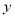， 满足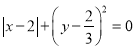，求（1）中所得结果的值．

    （1）-x+y2；（2） 【解析】试题分析：（1）先去括号，再合并即可得到结论； （2）根据非负数的性质得到x，y的值，然后代入计算即可． 试题解析：：（1）A+C－B= +- = +- =-x+y2； （2）因为x，y满足 ∴x+2=0， 解得：x=-2，y=， 代入-x+y2=-（-2）+（）2=2+=.

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

    若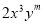与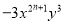是同类项，则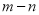的值是（ ）

    A. 3 B. 2 C. 1 D.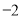

    B 【解析】试题解析：∵单项式与是同类项， ∴2n+1=3，m=3， ∴m=3，n=1， ∴m-n=2， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：解答题

    如图，点E是矩形ABCD边AB上一动点（不与点B重合），过点E作EF⊥DE交BC于点F，连接DF．已知AB = 4cm，AD = 2cm，设A，E两点间的距离为xcm，△DEF面积为ycm2．小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．

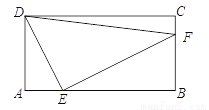
    下面是小明的探究过程，请补充完整：

    （1）确定自变量x的取值范围是 ；

    （2）通过取点、画图、测量、分析，得到了x与y的几组值，如下表：

    x/cm

    0

    0.5

    1

    1.5

    2

    2.5

    3

    3.5

    …

    y/cm2

    4.0

    3.7

    3.9

    3.8

    3.3

    2.0

    …

    （说明：补全表格时相关数值保留一位小数）

    （3）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；

    （4）结合画出的函数图象，解决问题：当△DEF面积最大时，AE的长度为 cm．

    （1）；（2）3.8，4.0；（3）画图见解析；（4）0或2. 【解析】试题分析：（1）根据点E是边AB上一动点（不与点B重合）即可得； （2）由题意可得△ADE∽△BEF，由相似三角形对应边成比例可以得到用x表示的BF，由y=S矩形ABCD -S△ADE-S△BEF-S△DCF 根据表格中的数据进行计算即可得； （3）根据表格中的数据进行描点，然后用平滑的曲线连接即可得； ...

    查看答案和解析>>

    科目：初中数学 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：填空题

    在北京市治理违建的过程中，某小区拆除了自建房，改建绿地. 如图，自建房占地是边长为8m的正方形ABCD，改建的绿地是矩形AEFG，其中点E在AB上，点G在AD的延长线上，且DG = 2BE. 如果设BE的长为x（单位：m），绿地AEFG的面积为y（单位：m2），那么y与x的函数的表达式为__________________；当BE =______m时，绿地AEFG的面积最大.

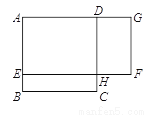
    2 【解析】由题意可知：AE=AB-BE=8-x，DG=2BE=2x，所以AG=AD+DG=8+2x， ∴y=AE·AG=（8-x）(8+2x)=-2x2+8x+64(0

    查看答案和解析>>

    科目：初中数学 来源：北京市丰台区2018届九年级第一学期期末数学试卷 题型：单选题

    已知抛物线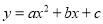上部分点的横坐标x与纵坐标y的对应值如下表：

    x

    …

    0

    1

    2

    3

    …

    y

    …

    3

    0

    m

    3

    …

    有以下几个结论：

    ①抛物线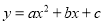的开口向下；②抛物线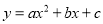的对称轴为直线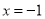；③方程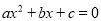的根为0和2；④当y＞0时，x的取值范围是x＜0或x＞2.其中正确的是（ ）

    A. ①④ B. ②④ C. ②③ D. ③④

    D 【解析】∵x=-1、3时的值相等， ∴x=0、2时的值相等，y=0，对称轴是直线x=1，故②错误； ∴方程的根为0和2，故③正确； 把(0，0)、（-1，3）、（1，-1）分别代入抛物线的解析式得： ， 解得： ，∴解析式为：y=x2-2x， ∴抛物线开口向上，故①错误； 当y＞0时，x的取值范围是x＜0或x＞2，故④正确， 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（人教版）：期中检测题 题型：填空题

    如果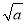的平方根是±3，则＝__________．

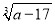    4 【解析】先利用平方根及算术平方根的定义求出a的值，再代入求值即可. 【解析】 ∵的平方根是±3， ∴＝9， ∴ ＝＝＝4. 故答案为：4.

    查看答案和解析>>

    科目：初中数学 来源：福建省泉州市2016-2017学年七年级下学期期末考试数学试卷 题型：解答题

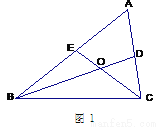
    （1）如图1，在△ABC中∠A＝60 º，BD、CE均为△ABC的角平分线且相交于点O.

    ①填空：∠BOC＝ 度；

    ②求证：BC＝BE+CD．(写出求证过程)

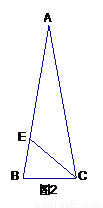
    （2）如图2，在△ABC中，AB=AC=m，BC=n， CE平分∠ACB．

    ①若△ABC的面积为S，在线段CE上找一点M，在线段AC上找一点N，使得AM+MN的值最小，则AM+MN的最小值是　　 　　　　．(直接写出答案)；　

    ②若∠A=20°，则△BCE的周长等于　　　　　　．(直接写出答案)．

    （1）①120；②证明见解析；（2）① (或)；②m 【解析】试题分析：（1）①根据三角形内角和定理得到∠BOC=180°-∠OBC-∠OCB，则2∠BOC=360°-2∠OBC-2∠OCB，再根据角平分线的定义得∠ABC=2∠OBC，∠ACB=2∠OCB，则2∠BOC=360°-∠ABC-∠ACB，易得∠BOC=90°+∠A，由∠A＝60 º即可得∠BOC的值； ②采用截长法在在BC...

    查看答案和解析>>

    同步练习册答案