
张强在一次投掷铅球时,刚出手时铅球离地面 m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图5所示:
m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图5所示:
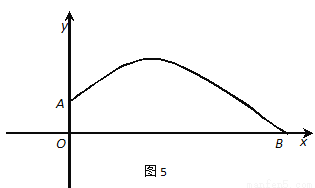
(1)请确定这个抛物线的顶点坐标
(2)求抛物线的函数关系式
(3)张强这次投掷成绩大约是多少?
(1)(4,3)(2)(3)张强这次投掷的成绩大约是10米 【解析】试题分析:(1)、根据水平距离和最大高度得出函数的顶点坐标;(2)、利用顶点和(0, 求出二次函数解析式;(3)、求出当y=0时x的值,从而得出成绩. 试题解析:(1)、(4,3); (2)、设抛物线的函数关系式为: , 因为顶点坐标为(4,3),所以有, 又因为点(0, 在抛物线上,所以有, ... 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:填空题
阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.
已知线段a,c如图.
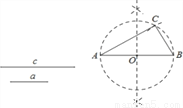
小芸的作法如下:
① 取AB=c,作AB的垂直平分线交AB于点O; ② 以点O为圆心,OB长为半径画圆;
③ 以点B为圆心,a长为半径画弧,与⊙O交于点C;④ 连接BC,AC.
则Rt△ABC即为所求.老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是________________________.
直径所对的圆周角为直角 【解析】试题分析:根据圆周角定理的推论求解. 【解析】 小芸的作法中判断∠ACB是直角的依据是直径所对的圆周角为直角. 故答案为:直径所对的圆周角为直角.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第23章小结与复习 测试 题型:填空题
在平行四边形、矩形、菱形、正方形、等腰梯形这五种图形中,既是轴对称图形,又是中心对称图形的是_____________.
矩形、菱形、正方形 【解析】本题主要考查了轴对称图形和中心对称图形的概念. 轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合. 根据轴对称图形和中心对称图形的概念作答. 【解析】 两者都是的是矩形,菱形,正方形; 其中平行四边形只是中心对称图形; 等腰梯形只是轴对称图形. 故既是轴对称,又是中心对称的...查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册 第23章 旋转 同步单元检测试卷(Word版附答案) 题型:单选题
如图,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=3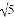 ,且∠ECF=45°,则CF的长为( )
,且∠ECF=45°,则CF的长为( )
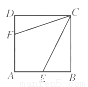
A. 2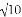 B. 3
B. 3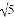 C.
C. 
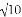 D.
D. 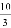
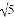
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册 第23章 旋转 同步单元检测试卷(Word版附答案) 题型:单选题
下列标志既是轴对称图形又是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:填空题
抛物线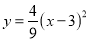 与x轴的交点为A,与y轴的交点为B,则三角形AOB的面积为____。
与x轴的交点为A,与y轴的交点为B,则三角形AOB的面积为____。
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:单选题
如图1,△ABC是直角三角形,∠A=90°,AB=8cm,AC=6cm点P从点A出发,沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,其中一个动点到达终点,则另一个动点也停止运动,则三角形APQ的最大面积是( )
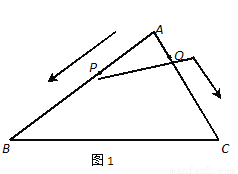
A. 8cm2 B. 16cm2 C. 24cm2 D. 32cm2
B 【解析】试题分析:根据题意可得:AP=2xcm,AQ=xcm,则S=,则根据题意可知:当x=4cm时,面积有最大值,最大面积为16.查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教八年级数学上册 第14章 章末综合检测 题型:单选题
下列因式分解,正确的是( )
A. x2y2-z2=x2(y+z)(y-z) B. -x2y+4xy-5y=-y(x2+4x+5)
C. (x+2)2-9=(x+5)(x-1) D. 9-12a+4a2=-(3-2a)2
【答案】C
【解析】解析:选项A.用平方差公式法,应为x2y2-z2=(xy+z)·(xy-z),故本选项错误.
选项B.用提公因式法,应为-x2y+ 4xy-5y=- y(x2- 4x+5),故本选项错误.
选项C.用平方差公式法,(x+2)2-9=(x+2+3)(x+2-3)=(x+5)(x-1),故本选项正确.
选项D.用完全平方公式法,应为9-12a+4a2=(3-2a)2,故本选项错误.
故选C.
点睛:(1)完全平方公式: 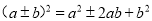 .
.
(2)平方差公式:(a+b)(a-b)= 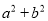 .
.
(3)常用等价变形: 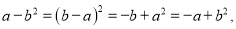
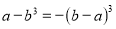 ,
,
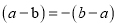 ,
,
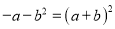 .
.
【题型】单选题
【结束】
10
已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
B 【解析】解析:∵2a4+2b4+c4=2a2c2+2b2c2,∴4a4-4a2c2+c4+4b4-4b2c2+c4=0, ∴(2a2-c2)2+(2b2-c2)2=0,∴2a2-c2=0,2b2-c2=0, ∴c=2a,c=2b, ∴a=b,且a2+b2=c2, ∴△ABC为等腰直角三角形. 故选B.查看答案和解析>>
科目:初中数学 来源:人教版数学八年级上册 第11章 11.3.1 多边形同步练习(解析版) 题型:单选题
若凸多边形的每个外角均为40°,过该多边形一个顶点的所有对角线条数是( )
A. 6 B. 8 C. 18 D. 27
A 【解析】这个多边形的边数是:360÷40=9, ∴过该多边形一个顶点的所有对角线条数是9﹣3=6条,故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com