
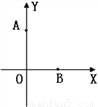
��ͼ��x�ᡢy������������ֱ���A(0,4)B(3,0)������x������һ��C��ʹ��ABCΪ���������Σ������������ĵ�C�У� ����
A. 2�� B. 3�� C. 4�� D. 5��
C ������������AP=AB����AΪԲ�ģ�ABΪ�뾶������x����1�����㣨A����⣩���������ABP�ǵ��������ε�P����1��������BP=AB����BΪԲ�ģ�BAΪ�뾶������x����2�����㣬�������ABP�ǵ��������ε�P����2��������PA=PB����AB�Ĵ�ֱƽ������x��ֻ��һ�����㣬�������ABP�ǵ��������ε�P����1�������Ե�P��x���ϣ���ABP�ǵ��������Σ����������ĵ�P����4������ѡC.
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017��������������п���ѧ��ģ�Ծ� ���ͣ���ѡ��
���м�����ȷ���ǣ�������
A. a2•a3=a6 B. ��a+b����a��2b��=a2��2b2
C. ��ab3��2=a2b6 D. 5a��2a=3
C ���������������������ͬ�����ݵij˷���������Զ���ʽ�ķ����ij˷����ݵij˷������Լ������̵����㷨��������м��㣬������ô𰸣� ���������A��a2•a3=a5���ʱ�ѡ����� B����a+b����a-2b��=a2��ab-2b2���ʱ�ѡ����� C����ab3��2=a2b6,��ѡ����ȷ�� D��5a-2a=3a���ʱ�ѡ����� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�������ʡ���������ɱ���2017����꼶��ѧ����ĩ��ѧ�Ծ� ���ͣ������
����ʽ��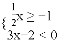 �Ľ⼯Ϊ________��
�Ľ⼯Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ��ɽ��2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
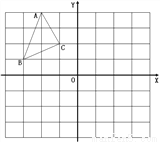
��ͼ��ƽ��ֱ������ϵ�У���ABC�������������ֱ�ΪA(-2,4)��B(-3,1)��C(-1,2)��
(1)������������A��B��C��,ʹ�����ABC����y��Գơ���д����A��B��C��������������ꡣ
(2)����ı���ABB��A���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ��ɽ��2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
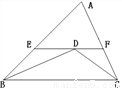
��ͼ����ABC�У���ABC���ACB��ƽ�����ཻ�ڵ�ģ��������ֱ��EF��BC����AB�ڵ�E����AC�ڵ�F��BE������EF��������FC��____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ��ɽ��2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��M(5,y)���N(x��-6)����x��Գƣ���x��y��ֵ�ֱ�Ϊ�� ��
A. 5����6 B. 5��6 C. ��5����6 D. ��5��6
B ����������֪��M(5,y)���N(x��-6)����x��Գƣ��ɵ�x=5��y=6����ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶�˽̰���ѧ�Ծ���C���� ���ͣ������
��ͼ������ֱ�ǡ�ABC�У���ABC=90�㣬��P��AC�ϣ�����ABP�ƶ���B��˳ʱ�뷽����ת90���õ���CBQ.
(1)���PCQ�Ķ���;
(2)��AB=4��AP��BP=1��3ʱ����PQ�ij���
(3)����P���߶�AC���˶�ʱ(P����A��C�غ�)����д��һ����ӳPA2��PC2��PB2֮���ϵ�ĵ�ʽ��������֤��.
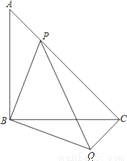
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶�˽̰���ѧ�Ծ���C���� ���ͣ���ѡ��
��ͼ��һ�������ߣ�y=��x��x��2����0��x��2����ΪC1������x�ύ������O��A1����C1��A1��ת180��õ�C2����x����A2����C2��A2��ת180��õ�C3����x����A3������˽�����ȥ���õ�Cn������P��2017��m����������Cn�ϣ���mΪ�� ��
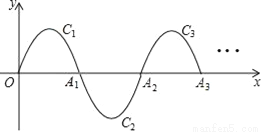
A. 1 B. ��1 C. 2 D. ��2
A ����������һ�������ߣ�y=-x��x-2����0��x��2���� ��ͼ����x�ύ������Ϊ����0��0������2��0���� �߽�C1�Ƶ�A1��ת180���C2����x���ڵ�A2�� ��C2�Ƶ�A2��ת180���C3����x���ڵ�A3�� �� ��˽�����ȥ��ֱ����Cn�� ��2017��2=1008����1�� ���P��2017��m����C1009�ϣ� ��C1009����x���...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ������
��ͼ����ABC�У�AD��BC��D����BD=AD��FD=CD�����룺BF��AC�Ĺ�ϵ����֤����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com